


Next: The Intermediate Vector Boson
Up: Examples
Previous: The Hadronic Current
For the phenomenological treatment of weak interactions we have
the current-current effective Lagrangian (77). It is
found that the known semileptonic and leptonic processes are well
described by the matrix elements of the Lagrangian at first order
of perturbation theory. Nevertheless, there are doubts about the
behaviour of higher orders. That is to say, the renormalization
properties (of theoretical interest) of the theory so formulated.
It is found that the theory is not renormalizable because too many
divergences appear. So it is valid to question where, at which
energy scale, these divergences will turn unsustainable. That is
to say where this model will stop having any value, even a
phenomenological one.
A typical process to study is
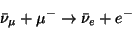 |
(101) |
whose first order cross section, as a dimensional analysis
shows, is
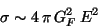 |
(102) |
On the other hand, the optical theorem at high energies allows to write
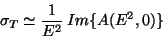 |
(103) |
where 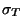 is the total cross section for
is the total cross section for
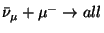 and
and  is the amplitude for elastic forward dispersion which is written,
without taking into account the spin dependence, from
is the amplitude for elastic forward dispersion which is written,
without taking into account the spin dependence, from
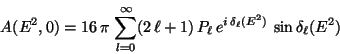 |
(104) |
But in the process we are dealing with, one finds that in the angular
distribution only the  waves are important, therefore
waves are important, therefore
 |
(105) |
Taking this result to (105) we have:
 |
(106) |
and so expression (104), calculated perturbatively at first order, can
be correct only for energies such that
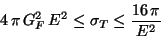 |
(107) |
that is to say
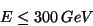 |
(108) |
called unitarity limit as it is provided by the optical theorem. In
conclusion, from a certain energy of the order given by (110), the
limit imposed by unitarity is violated and the effective model of
four fermions point interaction lacks sense.
In order to obtain some inspiration to continue it is interesting to
compare the behaviour of a similar process but this time of the
quantum electrodynamics. For instance
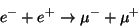 |
(109) |
In this case the interaction is electromagnetic and is mediated by the
photon:
Figure 12:
Photon mediated process
|
|
and the interaction terms are
The first order cross section of the process results
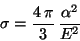 |
(110) |
decreasing with the energy as unitarity requires.
The conclusions of this comparison will be clearer from a short
dimensional analysis. Under the election
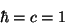 |
(111) |
it results
![\begin{displaymath}[M]= [\ell]^{-1} = [ t]^{-1}
\end{displaymath}](img286.gif) |
(112) |
and the exponent of ![$[M]$](img287.gif) is called dimension. Then it results, for example
is called dimension. Then it results, for example
![\begin{displaymath}[{\cal L}]= 4\;;\;[\psi] = 3/2
\end{displaymath}](img288.gif) |
(113) |
In particular one has
![\begin{displaymath}[e]= 0
\end{displaymath}](img289.gif) |
(114) |
which turns evident the origin of the behaviour (112).
Summarizing, inspiration came: the necessity of searching for a
theory of weak interactions involving a dimensionless coupling
constant and a mediator of the interaction is clear.



Next: The Intermediate Vector Boson
Up: Examples
Previous: The Hadronic Current
root
2001-01-22
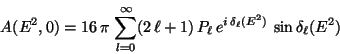
![]() waves are important, therefore
waves are important, therefore