


Next: Local Phase Invariance
Up: Examples
Previous: Parenthesis on Global and
It is the simplest case: one parameter group symmetry. Given the
Lagrangian of a complex scalar field
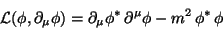 |
(149) |
invariant in front of the phase transformation, corresponding to the
group 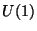
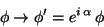 |
(150) |
which for the infinitesimal case it is reduced to
 |
(151) |
so that
The Noether theorem implies the conservation of the current
![\begin{displaymath}
J_{\mu} = i [\partial_{\mu} \phi^{\ast} \phi - \phi^{\ast} \partial_{\mu}\phi]
\end{displaymath}](img359.gif) |
(154) |
which allows to define a conserved charge
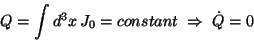 |
(155) |
which is the ``charge" of the field.
Real fields can be introduced through the transformations
in such a way that the Lagrangian is separated as
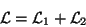 |
(158) |
with
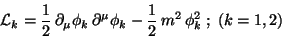 |
(159) |
which is the Lagrangian of a real scalar field.
The phase transformation implies in this notation
that is to say, a rotation in the plane
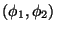 .
.
The phase invariance under (152) means that
the fields are not physically distinguishable. One can call
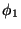 or
or 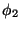 to any pair of
orthogonal combinations of the original fields. This fact
indicates the existence of a global symmetry. It is called global
because the change of phase of the fields is the same for all the
points
to any pair of
orthogonal combinations of the original fields. This fact
indicates the existence of a global symmetry. It is called global
because the change of phase of the fields is the same for all the
points 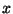 of the space-time.
of the space-time.
This idea of global symmetry can be extended to more complicated
phase transformations, with group structure depending on more
parameters. For example the case of the isospin, that is to say a
symmetry group 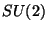 .
.
In this case the particle fields can be grouped in multiplets and the phase
transformation is, instead of (152), of the form
 |
(162) |
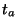 : matrix of appropriated dimension characteristic of the symmetry
group
: matrix of appropriated dimension characteristic of the symmetry
group 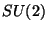 .
.
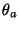 : constant parameters.
: constant parameters.



Next: Local Phase Invariance
Up: Examples
Previous: Parenthesis on Global and
root
2001-01-22
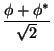
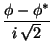
![]() or
or ![]() to any pair of
orthogonal combinations of the original fields. This fact
indicates the existence of a global symmetry. It is called global
because the change of phase of the fields is the same for all the
points
to any pair of
orthogonal combinations of the original fields. This fact
indicates the existence of a global symmetry. It is called global
because the change of phase of the fields is the same for all the
points ![]() of the space-time.
of the space-time.
![]() .
.
![]() : matrix of appropriated dimension characteristic of the symmetry
group
: matrix of appropriated dimension characteristic of the symmetry
group ![]() .
.
![]() : constant parameters.
: constant parameters.