


Next: Parenthesis on Isospin and
Up: The Standard Model of
Previous: Local Phase Invariance
This is the story of the fields that induce interactions when
acting as preservers of a local phase transformation.
If a local phase transformation linked to the 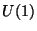 group
group
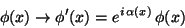 |
(165) |
is performed in the Lagrangian
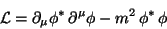 |
(166) |
the mass term presents no difficulties, it is trivially invariant in
front of the transformation (167). But what happens with the term
involving derivatives? In this case one has
![\begin{displaymath}
\partial_{\mu}\phi(x) \rightarrow \partial_{\mu}(e^{i \alph...
...ha(x)} [\partial_{\mu} + i \partial_{\mu}\alpha(x)] \phi(x)
\end{displaymath}](img387.gif) |
(167) |
so that
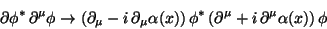 |
(168) |
and therefore the Lagrangian (168)
is not invariant under second class (local) gauge transformations
due to the contribution of the gradient of 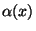 .
.
How could one turn 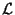 to be invariant?
to be invariant?
Remember that the electromagnetic field 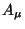 is defined modulus a gradient as
a consequence of the gauge invariance of electromagnetism. Then it is possible
that the invariance of
is defined modulus a gradient as
a consequence of the gauge invariance of electromagnetism. Then it is possible
that the invariance of 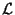 in front of local phase transformations
can be
restored taking advantage of the freedom of election of
in front of local phase transformations
can be
restored taking advantage of the freedom of election of 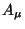 . How?,
adding
this electromagnetic field as a compensating term in the derivative
. How?,
adding
this electromagnetic field as a compensating term in the derivative
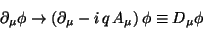 |
(169) |
which defines the so called gauge covariant derivative 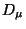 .
It is clear that when
.
It is clear that when  changes due to a transformation according to
(167), simultaneously the field
changes due to a transformation according to
(167), simultaneously the field 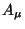 is required to change as
is required to change as
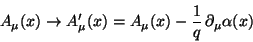 |
(170) |
Let us notice that 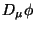 transforms in the same way as the
field
transforms in the same way as the
field  , that is
, that is
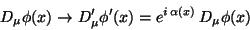 |
(171) |
It is then concluded that the Lagrangian
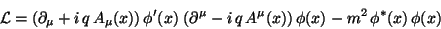 |
(172) |
is local phase transformation invariant. The field 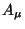 is
called gauge field. It is a compensating field to restore
the symmetry and a comparative field because its presence allows
to physically distinguish the particles of different charges, that
is to say it gives physical meaning to the charge attribute.
is
called gauge field. It is a compensating field to restore
the symmetry and a comparative field because its presence allows
to physically distinguish the particles of different charges, that
is to say it gives physical meaning to the charge attribute.
The immediate consequence of the requirement of invariance
under local phase transformations is the natural appearance of the
minimal interaction between the charged particles (charged fields)
and the electromagnetic or gauge field 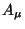 .
.
If we start now from a Lagrangian for fermions with mass 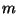 -
electrons for example -
-
electrons for example -
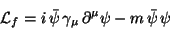 |
(173) |
the invariant Lagrangian in front of gauge transformations of second
class is
 |
(174) |
or equivalently
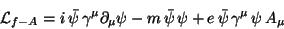 |
(175) |
where the appearance of the minimal interaction, as a consequence of
the requirement of a local phase symmetry or gauge symmetry is again
clear.



Next: Parenthesis on Isospin and
Up: The Standard Model of
Previous: Local Phase Invariance
root
2001-01-22
![]() group
group
![]() to be invariant?
to be invariant?
![]() is defined modulus a gradient as
a consequence of the gauge invariance of electromagnetism. Then it is possible
that the invariance of
is defined modulus a gradient as
a consequence of the gauge invariance of electromagnetism. Then it is possible
that the invariance of ![]() in front of local phase transformations
can be
restored taking advantage of the freedom of election of
in front of local phase transformations
can be
restored taking advantage of the freedom of election of ![]() . How?,
adding
this electromagnetic field as a compensating term in the derivative
. How?,
adding
this electromagnetic field as a compensating term in the derivative
![]() transforms in the same way as the
field
transforms in the same way as the
field ![]() , that is
, that is
![]() .
.
![]() -
electrons for example -
-
electrons for example -