Parenthesis on Isospin and Isotopic Invariance

Hadrons can be grouped in multiplets, for example

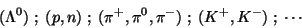$$(\Lambda^{0})\;;\;(p,n)\;;\;(\pi^{+},\pi^{0},\pi^{-})\;;\;(K^{+},K^{-})\;;\;\cdots$$ (176)

defined by certain quantum numbers common to its members. All the members of a given multiplete have the same 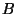$B$ (baryon number), 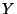$Y$ (hypercharge) (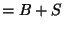$= B+S$ (strangeness)), 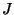$J$ (spin) and differ by the electric charge. Besides, it can be noticed that the masses of the members of a given multiplet are almost equal, although not identical.

The strong interactions of the members of a given multiplet are practically equal, for example the scattering amplitudes

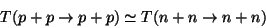$$T(p + p \rightarrow p + p) \simeq T(n + n \rightarrow n + n)$$ (177)

this indicates that the nuclear forces are independent of the electric charge of the interacting particles. In other words, in the absence (hypothetic) of electromagnetic interactions there would be no distinction between the proton state and the neutron state.

Summarizing, we find the existence of a symmetry indicating the possibility of giving a classification group to assign the particles the appropriated quantum numbers. Which group $G$ would it be? As the spin is common to all the members of a multiplet, one has in principle

$$[G,Poincar\acute{e}]= 0$$ (178)

implying then that the masses are equal in the multiplet. Therefore, this symmetry will be an approximated symmetry as this property is not fulfilled exactly.