


Next: The Nucleon Doublet
Up: Parenthesis on Isospin and
Previous: Parenthesis on Isospin and
This is the group, non abelian, of of 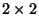 complex matrices
complex matrices  which verify
which verify
![\begin{displaymath}
\begin{array}{rll}
U^{\dagger} U & = U U^{\dagger} = 1 &\;;\;[unitary] \\
\det U & = 1 &\;;\;[unimodular]
\end{array}\end{displaymath}](img411.gif) |
(179) |
This group depends on three continuous parameters
 . The elements of the group can be written
. The elements of the group can be written
![\begin{displaymath}
U = exp [i \sum_{j}I_{j} \alpha_{j}] = e^{i I_{j} \alpha_{j}}
\end{displaymath}](img413.gif) |
(180) |
with
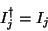 |
(181) |
and
 |
(182) |
A possible election of 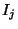 is
is
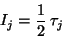 |
(183) |
where 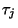 are the Pauli matrices which verify the commutation rules
are the Pauli matrices which verify the commutation rules
![\begin{displaymath}[\frac{1}{2} \tau_{i},\frac{1}{2} \tau_{j}]= i \epsilon_{ijk}
\frac{1}{2} \tau_{k}
\end{displaymath}](img419.gif) |
(184) |
Writing an infinitesimal transformation
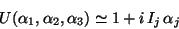 |
(185) |
it is clear that the
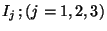 are the generators of the group.
are the generators of the group.
The Lie theorem, which shows that the commutation
rules are valid independently of the representation of the generators,
allows to write
![\begin{displaymath}[I_{i},I_{j}]= i \epsilon_{ijk} I_{k}
\end{displaymath}](img422.gif) |
(186) |
and therefore
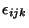 are the structure constants of the
non abelian Lie algebra of SU(2).
are the structure constants of the
non abelian Lie algebra of SU(2).
There exists an operator which commutates with the three
generators
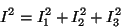 |
(187) |
which is the Casimir operator of the group. As a consequence, the
irreducible representations of 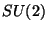 are characterized by the
eigenvalues of
are characterized by the
eigenvalues of 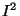 . Resulting
. Resulting
with
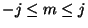 . The states
. The states 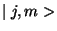 belong to an irreducible
basis of dimension
belong to an irreducible
basis of dimension 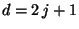 .
.
There exists also an empirical relation of Gell-Mann and Nishijima for the
electric charge of a particle, namely
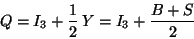 |
(190) |
That makes clear then, from the commutation relations, that
![\begin{displaymath}[Q,I_{j}]\neq 0 \;;\; for\;j=1,2
\end{displaymath}](img434.gif) |
(191) |
that is to say, the electric charge breakes the conservation of
isospin as it should be expected.



Next: The Nucleon Doublet
Up: Parenthesis on Isospin and
Previous: Parenthesis on Isospin and
root
2001-01-22
![]() complex matrices
complex matrices ![]() which verify
which verify
![]() is
is