


Next: Yang-Mills Fields
Up: Parenthesis on Isospin and
Previous: The SU(2) Group
In the absence of electromagnetic interaction the proton and the
neutron are practically identical and can be considered as states of a
more fundamental entity, the nucleon. For this one the quantum state
can be written
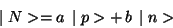 |
(192) |
where 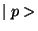 is the proton state and
is the proton state and  the neutron state,
respectively. The constants
the neutron state,
respectively. The constants
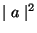 and
and
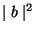 measure the probability of finding a nucleon as proton or as neutron
respectively. The two different charge states
measure the probability of finding a nucleon as proton or as neutron
respectively. The two different charge states 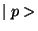 and
and  are eigenstates of
are eigenstates of
 |
(193) |
with eigenvalues 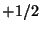 and
and 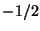 respectively.
respectively.
The following operators are also introduced
which change from the neutron state to the proton state and vice versa.
The complete state of the nucleon will be
 |
(196) |
where
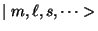 is the state defined by the corresponding
dynamical attributes and
is the state defined by the corresponding
dynamical attributes and 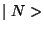 the nucleon state of the isospace
defined in (194) and determined by two quantum numbers:
the nucleon state of the isospace
defined in (194) and determined by two quantum numbers: 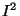 and
and  .
.
The isospin symmetry - present when there is no electromagnetism
- implies that there exists a unitary group 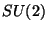 , of transformations
in the Hilbert space of the state vectors so that
, of transformations
in the Hilbert space of the state vectors so that
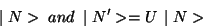 |
(197) |
or in the general case
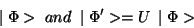 |
(198) |
define the same phenomenon when only the strong interactions are
present.
If now the case is a physical observable represented by an
operator 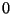 and
and 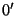 is the observable after an isospin transformation, one
must have
is the observable after an isospin transformation, one
must have
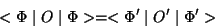 |
(199) |
that using the definition of  leads to
leads to
 |
(200) |
which is the typical form of transformation of an operator.
If we deal now with the field theory of a nucleon, its state will
be presented by the field
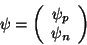 |
(201) |
which is a double spinor - 8 components - composition of the proton spinor
with the neutron spinor. As the field has the character of operator,
it is transformed under isospin as
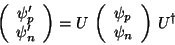 |
(202) |
but as the fields of the proton and of the neutron are components of an
irreducible tensorial operator of order 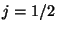 , the transformation
(204) has the form
, the transformation
(204) has the form
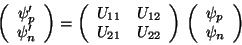 |
(203) |
Note: 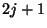 operators
operators 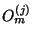 which act in the vector
space of the irreducible representation of dimension
which act in the vector
space of the irreducible representation of dimension 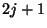 form the
components of an irreducible tensorial operator of order
form the
components of an irreducible tensorial operator of order 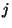 if they are transformed as
if they are transformed as
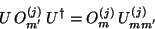 |
(204) |
where 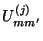 is the representation of the transformation group.
is the representation of the transformation group.
The unitarity of 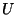 implies that the anticommutation relations of
the fermionic fields of the nucleon are conserved in a transformation
of isospin.
implies that the anticommutation relations of
the fermionic fields of the nucleon are conserved in a transformation
of isospin.
Using now
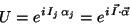 |
(205) |
which for the 1/2 representation is
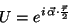 |
(206) |
the isotopic infinitesimal transformation of the nucleon finally results
 |
(207) |
Clearly, any further generalization to include  can be done inmediatly.
can be done inmediatly.



Next: Yang-Mills Fields
Up: Parenthesis on Isospin and
Previous: The SU(2) Group
root
2001-01-22
![]() , of transformations
in the Hilbert space of the state vectors so that
, of transformations
in the Hilbert space of the state vectors so that
![]() and
and ![]() is the observable after an isospin transformation, one
must have
is the observable after an isospin transformation, one
must have
![]() operators
operators ![]() which act in the vector
space of the irreducible representation of dimension
which act in the vector
space of the irreducible representation of dimension ![]() form the
components of an irreducible tensorial operator of order
form the
components of an irreducible tensorial operator of order ![]() if they are transformed as
if they are transformed as
![]() implies that the anticommutation relations of
the fermionic fields of the nucleon are conserved in a transformation
of isospin.
implies that the anticommutation relations of
the fermionic fields of the nucleon are conserved in a transformation
of isospin.
![]() can be done inmediatly.
can be done inmediatly.