


Next: Orbifold Compactifications
Up: SUPERSTRING PHENOMENOLOGY BEFORE 1995
Previous: String Model Building
In order to construct string models in less than 10D as well as to
understand the heterotic string construction, we need to
consider the simplest compactifications which correspond to the extra
dimensions being circles and their higher dimensional generalization.
Let us first see the case of a circle. This means that the 10D space
is represented by flat 9D spacetime times a circle 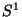 . We know that a
circle is just the real line identifying all the numbers differing by
. We know that a
circle is just the real line identifying all the numbers differing by 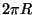 ,
where
,
where 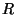 is the radius of the circle.
So the only difference with the flat space discussed above are the boundary conditions. The solution of the wave equations are now as in (4).
But now
is the radius of the circle.
So the only difference with the flat space discussed above are the boundary conditions. The solution of the wave equations are now as in (4).
But now 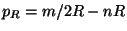 and
and  ,
, 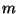 is an integer
reflecting the fact that the momentum in the compact
direction has to be quantized in order to get single-valued
wave function. The integer
is an integer
reflecting the fact that the momentum in the compact
direction has to be quantized in order to get single-valued
wave function. The integer  however refers to the fact that
the string can wind around several times in the compact dimension and is thus
named the `winding number'. The mass formula is then:
however refers to the fact that
the string can wind around several times in the compact dimension and is thus
named the `winding number'. The mass formula is then:
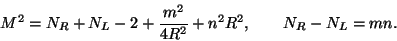 |
(6) |
This shows several interesting facts.
First, for  and varying
and varying 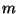 , we obtain an infinite
tower of massive states with masses
, we obtain an infinite
tower of massive states with masses 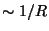 ; these are the
standard `momentum states' of Kaluza-Klein compactifications
in field theory. In particular the massless states with
; these are the
standard `momentum states' of Kaluza-Klein compactifications
in field theory. In particular the massless states with
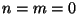 and one oscillator in the compact direction
are vector fields in the extra dimensions giving rise
to a
and one oscillator in the compact direction
are vector fields in the extra dimensions giving rise
to a
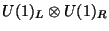 Kaluza-Klein gauge symmetry. The states with
Kaluza-Klein gauge symmetry. The states with 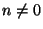 are
the winding states and are purely stringy; they represent
string states winding around the circle, they have
mass
are
the winding states and are purely stringy; they represent
string states winding around the circle, they have
mass 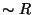 .
Second, there are special values of
.
Second, there are special values of 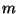 and
and  which can give rise
to extra massless states. In particular for
which can give rise
to extra massless states. In particular for 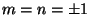 we can see that
at the special radius
we can see that
at the special radius  in units of
in units of 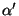 , there are massless states with a single
oscillator
, there are massless states with a single
oscillator  corresponding to massless vectors which in this
case generate
corresponding to massless vectors which in this
case generate
 . This means that the special point
in the `moduli space' of the circle
. This means that the special point
in the `moduli space' of the circle  is a point of enhanced symmetry.
The original
is a point of enhanced symmetry.
The original
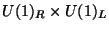 Kaluza-Klein symmetry of compactification on a circle gets enhanced to
Kaluza-Klein symmetry of compactification on a circle gets enhanced to
 . This is a very stringy effect because it depends crucially on the existence of winding modes
(
. This is a very stringy effect because it depends crucially on the existence of winding modes
(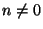 ).
The third interesting fact about this compactification is that the spectrum
is invariant under the following `duality' transformations [8]:
).
The third interesting fact about this compactification is that the spectrum
is invariant under the following `duality' transformations [8]:
 |
(7) |
This is also a stringy property. It exchanges small
with large distances but at the same time it
exchanges momentum (Kaluza-Klein) states with
winding states. This symmetry can be shown to hold not
only for the spectrum but also for the interactions and
therefore it is an exact symmetry of string perturbation theory.
Let us now extend the compactification to two dimensions, i.e.,
the 26D spacetime is the product of flat 24D spacetime and a
2D generalization of a circle, the torus  . Again the only difference with flat space is the boundary
conditions. The two compact dimensions are identified by
vectors of a 2D lattice, defining the torus
. Again the only difference with flat space is the boundary
conditions. The two compact dimensions are identified by
vectors of a 2D lattice, defining the torus  .
Out of the three independent components of the compactified
metric
.
Out of the three independent components of the compactified
metric
 and the single component of
and the single component of
 namely
namely 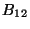 we can build two complex `moduli' fields:
we can build two complex `moduli' fields:
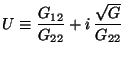 |
|
|
|
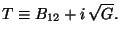 |
|
|
(8) |
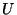 is the standard modular parameter of any geometrical
2D torus and it is usually identified as the `complex
structure' modulus.
is the standard modular parameter of any geometrical
2D torus and it is usually identified as the `complex
structure' modulus.  is the `Kähler structure' modulus
(since
is the `Kähler structure' modulus
(since  is a complex Kähler space) and its imaginary part
measures the overall size of the torus, since
is a complex Kähler space) and its imaginary part
measures the overall size of the torus, since  is the
determinant of the 2D metric. It plays the same role as
is the
determinant of the 2D metric. It plays the same role as 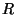 did for the 1D circle. In terms of
did for the 1D circle. In terms of  and
and 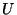 we can write the left- and
right-moving momenta as:
we can write the left- and
right-moving momenta as:
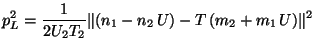 |
|
|
|
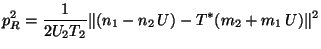 |
|
|
(9) |
The mass forula, depending on  , again shows that there are enhanced symmetry points for
special values of
, again shows that there are enhanced symmetry points for
special values of  and
and 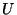 . It also shows the following symmetries:
. It also shows the following symmetries:
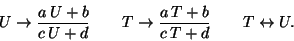 |
(10) |
Where 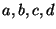 are integers satisfying
are integers satisfying 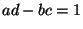 .
The first transformation is the standard
.
The first transformation is the standard
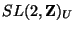 `modular' symmetry of 2D
tori and is independent of string theory; it is purely geometric.
The second transformation is a stringy
`modular' symmetry of 2D
tori and is independent of string theory; it is purely geometric.
The second transformation is a stringy
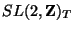 named
named
 -duality and it is a generalization of (7)
for the 2D case. Again this is a symmetry as long as we also transform
momenta
-duality and it is a generalization of (7)
for the 2D case. Again this is a symmetry as long as we also transform
momenta 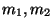 with winding
with winding 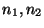 .
The third symmetry exchanges the
complex structure
.
The third symmetry exchanges the
complex structure 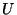 with the Kähler structure
with the Kähler structure  and
it is called `mirror symmetry'.
If
and
it is called `mirror symmetry'.
If 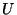 and
and  each parametrize a complex plane
each parametrize a complex plane
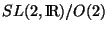 , the duality symmetry implies that they can only live
in the fundamental domain defined by all the points of the product of complex spaces
, the duality symmetry implies that they can only live
in the fundamental domain defined by all the points of the product of complex spaces
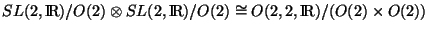 identified under the
duality group
identified under the
duality group
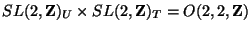 .
.
This is the situation that gets generalized to higher dimensions.
In general, compactification on a 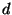 -dimensional torus has the
moduli space
-dimensional torus has the
moduli space
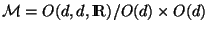 with
points identified under the duality group
with
points identified under the duality group
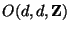 .
For the heterotic string with 16 extra left moving coordinates
.
For the heterotic string with 16 extra left moving coordinates
 with
a similar modification to the duality group.
The left- and right- moving momenta
with
a similar modification to the duality group.
The left- and right- moving momenta 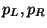 live on an
even, selfdual lattice of signature
live on an
even, selfdual lattice of signature  , which
is usually called the Narain lattice
, which
is usually called the Narain lattice
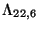 [9].
This generalizes the
[9].
This generalizes the 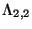 lattice defined by the
integers
lattice defined by the
integers
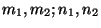 of eq. (9).
of eq. (9).
We can easily verify in this case that the dimension of
 is
is 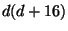 corresponding to the number of independent
components of
corresponding to the number of independent
components of
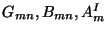 with
with
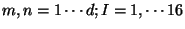 . For
. For 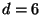 we have a
4D string model with a moduli space of dimension
we have a
4D string model with a moduli space of dimension 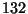 . To
this we have to add the dilaton field
. To
this we have to add the dilaton field 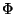 which, together
with the spacetime components of the antisymmetric
tensor
which, together
with the spacetime components of the antisymmetric
tensor  , can be combined into a new modular
parameter:
, can be combined into a new modular
parameter:
 |
(11) |
Here the axion field 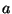 is defined as
is defined as
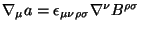 .
.
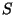 parametrizes again a coset
parametrizes again a coset
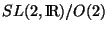 . It is then natural to
believe there is also a duality symmetry for the field
. It is then natural to
believe there is also a duality symmetry for the field 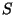 of the type
of the type 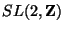 ; by analogy with the situation for
; by analogy with the situation for  and
and 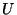 .
Such a symmetry was proposed in ref.[10] and it
has received a lot of attention recently. If true it
may have far reaching
consequences since (similar to equation (7)) it relates
strong to weak string coupling.
.
Such a symmetry was proposed in ref.[10] and it
has received a lot of attention recently. If true it
may have far reaching
consequences since (similar to equation (7)) it relates
strong to weak string coupling.



Next: Orbifold Compactifications
Up: SUPERSTRING PHENOMENOLOGY BEFORE 1995
Previous: String Model Building
root
2001-01-22
![]() . We know that a
circle is just the real line identifying all the numbers differing by
. We know that a
circle is just the real line identifying all the numbers differing by ![]() ,
where
,
where ![]() is the radius of the circle.
So the only difference with the flat space discussed above are the boundary conditions. The solution of the wave equations are now as in (4).
But now
is the radius of the circle.
So the only difference with the flat space discussed above are the boundary conditions. The solution of the wave equations are now as in (4).
But now ![]() and
and ![]() ,
, ![]() is an integer
reflecting the fact that the momentum in the compact
direction has to be quantized in order to get single-valued
wave function. The integer
is an integer
reflecting the fact that the momentum in the compact
direction has to be quantized in order to get single-valued
wave function. The integer ![]() however refers to the fact that
the string can wind around several times in the compact dimension and is thus
named the `winding number'. The mass formula is then:
however refers to the fact that
the string can wind around several times in the compact dimension and is thus
named the `winding number'. The mass formula is then:
![\includegraphics[width=4in,height=2.5in]{mexfigtor.eps}](img71.gif)
![]() . Again the only difference with flat space is the boundary
conditions. The two compact dimensions are identified by
vectors of a 2D lattice, defining the torus
. Again the only difference with flat space is the boundary
conditions. The two compact dimensions are identified by
vectors of a 2D lattice, defining the torus ![]() .
Out of the three independent components of the compactified
metric
.
Out of the three independent components of the compactified
metric
![]() and the single component of
and the single component of
![]() namely
namely ![]() we can build two complex `moduli' fields:
we can build two complex `moduli' fields:
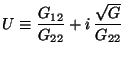
![]() -dimensional torus has the
moduli space
-dimensional torus has the
moduli space
![]() with
points identified under the duality group
with
points identified under the duality group
![]() .
For the heterotic string with 16 extra left moving coordinates
.
For the heterotic string with 16 extra left moving coordinates
![]() with
a similar modification to the duality group.
The left- and right- moving momenta
with
a similar modification to the duality group.
The left- and right- moving momenta ![]() live on an
even, selfdual lattice of signature
live on an
even, selfdual lattice of signature ![]() , which
is usually called the Narain lattice
, which
is usually called the Narain lattice
![]() [9].
This generalizes the
[9].
This generalizes the ![]() lattice defined by the
integers
lattice defined by the
integers
![]() of eq. (9).
of eq. (9).
![]() is
is ![]() corresponding to the number of independent
components of
corresponding to the number of independent
components of
![]() with
with
![]() . For
. For ![]() we have a
4D string model with a moduli space of dimension
we have a
4D string model with a moduli space of dimension ![]() . To
this we have to add the dilaton field
. To
this we have to add the dilaton field ![]() which, together
with the spacetime components of the antisymmetric
tensor
which, together
with the spacetime components of the antisymmetric
tensor ![]() , can be combined into a new modular
parameter:
, can be combined into a new modular
parameter: