


Next: F-Theory
Up: Non-perturbative String Theory
Previous: M-Theory
Just as the M-theory compactification on 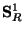 leads to the Type IIA theory,
Horava and Witten realized that orbifold compactifications leads to the
leads to the Type IIA theory,
Horava and Witten realized that orbifold compactifications leads to the
 heterotic theory in ten dimensions HE (see for instance [23]). More precisely
heterotic theory in ten dimensions HE (see for instance [23]). More precisely
 |
(56) |
where
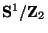 is homeomorphic to the finite interval
is homeomorphic to the finite interval  and the
and the
 -theory is thus defined on
-theory is thus defined on 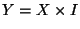 . From the ten-dimensional point of
view, this configuration is seen as two parallel planes placed at the two boundaries
. From the ten-dimensional point of
view, this configuration is seen as two parallel planes placed at the two boundaries
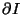 of
of  . Dimensional reduction and anomalies cancellation conditions imply
that the gauge degrees of freedom should be trapped on the ten-dimensional planes
. Dimensional reduction and anomalies cancellation conditions imply
that the gauge degrees of freedom should be trapped on the ten-dimensional planes 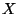 with the gauge group being
with the gauge group being 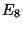 in each plane. While that the gravity is propagating
in the bulk and thus both copies of
in each plane. While that the gravity is propagating
in the bulk and thus both copies of 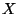 's are only connected gravitationally.
truecm
's are only connected gravitationally.
truecm
root
2001-01-15