



Next: Sobre este documento...
Up: tglo
Previous: Bibliografía
Índice General
Dada la trimétrica
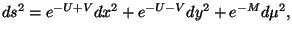 se procede a obtener los símbolos de Christoffel, dados por la
siguiente ecuación
se procede a obtener los símbolos de Christoffel, dados por la
siguiente ecuación
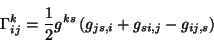 |
(A.1) |
De los 27
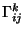 , aquellos que son diferentes de cero son
, aquellos que son diferentes de cero son
Con lo anterior se puede encontrar el tensor de Riemann
mediante la expresión
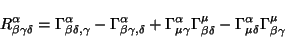 |
(A.3) |
Las componentes diferentes de cero son las siguientes
Con lo anterior se calcula el tensor de Ricci, que se encuentra
contrayendo el tensor de Riemann, esto es
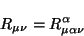 |
(A.5) |
esta ecuación da el siguiente resultado
Finalmente, el escalar de curvatura está dado por




Next: Sobre este documento...
Up: tglo
Previous: Bibliografía
Índice General
enrique pazos
2000-09-27
![]() se procede a obtener los símbolos de Christoffel, dados por la
siguiente ecuación
se procede a obtener los símbolos de Christoffel, dados por la
siguiente ecuación