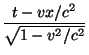Next: Intervalo de espacio-tiempo
Up: INTRODUCCIÓN A LA TEORÍA
Previous: INTRODUCCIÓN A LA TEORÍA
Índice General
Un sistema de referencia inercial se define como aquel en el cual se cumple
la primera ley de Newton. Esta ley establece que un cuerpo sobre el cual
actúe una fuerza externa neta igual a cero se moverá con velocidad
constante. La relación existente entre las coordenadas de dos sistemas
inerciales en movimiento relativo está dada por las transformaciones de Galileo para el movimiento en una dimensión
Una de las particularidades de este tipo de transformaciones es que el
parámetro 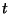 es el mismo en cualquier sistema de coordenadas. De estas
ecuaciones se deriva que la aceleración de una partícula medida en
ambos sistemas es la misma. En física clásica, el movimiento del
sistema de referencia no influye en la masa de la partícula. Por lo
tanto, la cantidad
es el mismo en cualquier sistema de coordenadas. De estas
ecuaciones se deriva que la aceleración de una partícula medida en
ambos sistemas es la misma. En física clásica, el movimiento del
sistema de referencia no influye en la masa de la partícula. Por lo
tanto, la cantidad 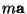 es igual para todos, es decir,
es igual para todos, es decir,
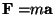 y
y
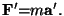 De esto se
concluye que
De esto se
concluye que
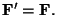 Las leyes newtonianas del
movimiento y las ecuaciones de movimiento de una partícula son
exactamente iguales en todos los sistemas inerciales.
Lo mismo se puede decir de los principios de conservación, puesto que
son derivables de las leyes de Newton. Esto significa que las leyes de la
mecánica clásica son iguales en todos los sistemas inerciales. Lo
anterior implica que ningún experimento mecánico efectuado dentro de
un sistema inercial, puede indicarle al observador cuál es el movimiento
de dicho sistema con respecto a cualquier otro sistema inercial. Del mismo
modo, no hay forma de determinar una velocidad absoluta en un sistema
inercial de referencia a partir de experimentos mecánicos. Al hecho de
que sólo se puede hablar de velocidad relativa de un sistema con
respecto al otro y no a la velocidad absoluta de un sistema, se le llama
relatividad newtoniana. [1]
A principios de este siglo se encontró que las ecuaciones de Maxwell
para el campo electromagnético no obedecían el principio de la
relatividad newtoniana, es decir, que no eran invariantes ante las
tranformaciones de Galileo. Esto quiere decir que los fenómenos
electromagnéticos en una nave en movimiento serían diferentes de
aquellos que se presentan en una nave estacionaria. Lo anterior implica que
usando fenómenos electromagnéticos se podría determinar la
velocidad absoluta de la nave.
Una de las consecuencias de la ecuaciones de Maxwell es que la luz se
propaga en todas direcciones a la misma velocidad
Las leyes newtonianas del
movimiento y las ecuaciones de movimiento de una partícula son
exactamente iguales en todos los sistemas inerciales.
Lo mismo se puede decir de los principios de conservación, puesto que
son derivables de las leyes de Newton. Esto significa que las leyes de la
mecánica clásica son iguales en todos los sistemas inerciales. Lo
anterior implica que ningún experimento mecánico efectuado dentro de
un sistema inercial, puede indicarle al observador cuál es el movimiento
de dicho sistema con respecto a cualquier otro sistema inercial. Del mismo
modo, no hay forma de determinar una velocidad absoluta en un sistema
inercial de referencia a partir de experimentos mecánicos. Al hecho de
que sólo se puede hablar de velocidad relativa de un sistema con
respecto al otro y no a la velocidad absoluta de un sistema, se le llama
relatividad newtoniana. [1]
A principios de este siglo se encontró que las ecuaciones de Maxwell
para el campo electromagnético no obedecían el principio de la
relatividad newtoniana, es decir, que no eran invariantes ante las
tranformaciones de Galileo. Esto quiere decir que los fenómenos
electromagnéticos en una nave en movimiento serían diferentes de
aquellos que se presentan en una nave estacionaria. Lo anterior implica que
usando fenómenos electromagnéticos se podría determinar la
velocidad absoluta de la nave.
Una de las consecuencias de la ecuaciones de Maxwell es que la luz se
propaga en todas direcciones a la misma velocidad 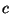 . Además, si la
fuente que emite la luz está en movimiento, la luz seguirá
propagándose con la misma velocidad
. Además, si la
fuente que emite la luz está en movimiento, la luz seguirá
propagándose con la misma velocidad 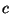 , lo cual contradice las leyes de
transformación de Galileo. Esto hizo necesario buscar otro tipo de
transformaciones que dejarán invariantes las ecuaciones de Maxwell. En
1903, Lorentz propuso otras leyes de transformación y las aplicó a
dichas ecuaciones, encontrando que éstas permanecían invariantes.
Las ecuaciones de transformación de Lorentz son las siguientes
, lo cual contradice las leyes de
transformación de Galileo. Esto hizo necesario buscar otro tipo de
transformaciones que dejarán invariantes las ecuaciones de Maxwell. En
1903, Lorentz propuso otras leyes de transformación y las aplicó a
dichas ecuaciones, encontrando que éstas permanecían invariantes.
Las ecuaciones de transformación de Lorentz son las siguientes
En 1905, Einstein generalizó el principio de la relatividad newtoniana a
toda la física estableciendo lo que se conoce como los postulados de la relatividad especial:
- Todos los marcos de referencia incercial son equivalentes para todos
los experimentos.
- La velocidad de la luz es constante en cualquier marco de referencia
inercial.
La idea de Einstein era evitar las inconsistencias entre las ecuaciones de
Maxwell y las transformaciones de Galileo. La relación correcta entre
espacio y tiempo estaría dada por las ecuaciones de Lorentz. [2]




Next: Intervalo de espacio-tiempo
Up: INTRODUCCIÓN A LA TEORÍA
Previous: INTRODUCCIÓN A LA TEORÍA
Índice General
enrique pazos
2000-09-27