Next: Principio de equivalencia
Up: INTRODUCCIÓN A LA TEORÍA
Previous: Primeras ideas de relatividad
Índice General
Sea 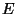 un evento con coordenadas
un evento con coordenadas
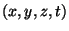 en el sistema
en el sistema 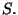 Este mismo evento visto desde un sistema de coordenadas
Este mismo evento visto desde un sistema de coordenadas 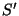 que se
mueve con una velocidad relativa en la dirección del eje
que se
mueve con una velocidad relativa en la dirección del eje 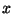 del sistema
del sistema
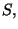 tendrá coordenadas
tendrá coordenadas
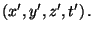 Asumiendo que en
Asumiendo que en
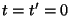 un rayo de luz
sale del origen de
un rayo de luz
sale del origen de 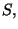 en ambos sistemas se cumple que
en ambos sistemas se cumple que
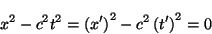 |
(1.3) |
Esto se cumple para cualquier evento pero el resultado no siempre es cero.
Aplicando las transformaciones de Lorentz se puede demostrar que para
cualquier evento
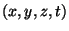 y
y
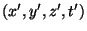 se cumple que
se cumple que
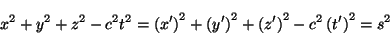 |
(1.4) |
donde 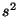 es el intervalo de espacio-tiempo y es invariante ante una
transformación de Lorentz. Si se consideran dos puntos
infinitesimalmente juntos, el cuadrado del intervalo
es el intervalo de espacio-tiempo y es invariante ante una
transformación de Lorentz. Si se consideran dos puntos
infinitesimalmente juntos, el cuadrado del intervalo 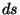 entre ellos se
conoce como métrica. [3] En forma general, la
métrica se expresa como
entre ellos se
conoce como métrica. [3] En forma general, la
métrica se expresa como
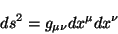 |
(1.5) |
donde 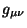 es el tensor métrico, que se verá en detalle
más adelante y
es el tensor métrico, que se verá en detalle
más adelante y 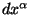 es el desplazamientos
infinitesimal de la coordenada
es el desplazamientos
infinitesimal de la coordenada 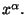 Los subíndices y superíndices con letras griegas expresan la
sumatoria sobre cuatro dimensiones. Aquellos que correspondan a letras
latinas denotan sumatoria sobre tres dimensiones. La notación que se
adoptará para desplazamientos contravariantes es
Los subíndices y superíndices con letras griegas expresan la
sumatoria sobre cuatro dimensiones. Aquellos que correspondan a letras
latinas denotan sumatoria sobre tres dimensiones. La notación que se
adoptará para desplazamientos contravariantes es
En el espacio de la relatividad especial la ec. 1.5 toma la forma
aquí,
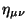 se conoce como tensor de Lorentz y sus
valores son
se conoce como tensor de Lorentz y sus
valores son
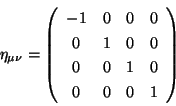 |
(1.8) |
De la ec. 1.7 se puede ver que 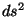 no siempre es
positivo. Existen tres casos posibles. Si
no siempre es
positivo. Existen tres casos posibles. Si 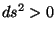 el intervalo se denomina
espacial, si
el intervalo se denomina
espacial, si 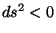 el intervalo es temporal y si
el intervalo es temporal y si 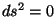 se denomina intervalo nulo. Este último es el que
corresponde a la trayectoria seguida por un rayo de luz. [3]
se denomina intervalo nulo. Este último es el que
corresponde a la trayectoria seguida por un rayo de luz. [3]




Next: Principio de equivalencia
Up: INTRODUCCIÓN A LA TEORÍA
Previous: Primeras ideas de relatividad
Índice General
enrique pazos
2000-09-27