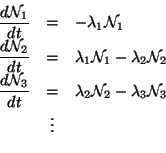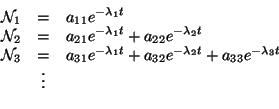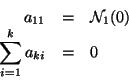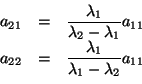Next: Elementos radiactivos naturales
Up: tesis
Previous: INTRODUCCIÓN
Índice General
La radiactividad fue descubierta en 1896 por Henri Becquerel cuando investigaba
la fluoresencia de ciertos compuestos después de ser expuestos a la luz solar.
Becquerel se percató accidentalmente
que el uranisulfito de potasio era capaz de velar placas fotográficas sin
necesidad de exponer el compuesto al sol y que su ``fluorecencia'' podía atravesar
las envolturas en las que se encontraba la placa fotográfica.
Pierre y Marie Curie continuaron con la investigación de Becquerel y descubrieron que
el torio tenía la misma propiedad del uranio y la llamaron radiactividad.
Los Curie descubrieron el polonio y el radio como nuevos elementos en la tabla
periódica.
Poco tiempo después Ernest Rutherford descubre que la radiación era un
fenómeno compuesto y descubrió las partículas alfa y beta.
En 1900 P. Villard descubre que un tercer componente de la
radiación que era mucho más penetrante que las partículas 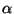 y
y 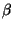 y que no era desviado por campos eléctricos ni magnéticos, por
lo que debía ser una onda electromagnética, a la que llamó rayos gamma.
En 1934 J.-F. Joliot y I. Joliot-Curie logra formar átomos de
y que no era desviado por campos eléctricos ni magnéticos, por
lo que debía ser una onda electromagnética, a la que llamó rayos gamma.
En 1934 J.-F. Joliot y I. Joliot-Curie logra formar átomos de 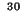 P radiactivos al
bombardear átomos de
P radiactivos al
bombardear átomos de 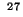 Al con partículas
Al con partículas 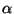 .
En 1942 Fermi y sus colaboradores construyen el primer reactor nuclear autosostenido
en el sótano de la universidad de Chicago con lo que la humanidad pudo
generar elementos radiactivos artificialmente.
La radiactividad es un proceso estocástico presente en la naturaleza en el cual un
núcleo atómico inestable decae por medio de la emisión partículas
.
En 1942 Fermi y sus colaboradores construyen el primer reactor nuclear autosostenido
en el sótano de la universidad de Chicago con lo que la humanidad pudo
generar elementos radiactivos artificialmente.
La radiactividad es un proceso estocástico presente en la naturaleza en el cual un
núcleo atómico inestable decae por medio de la emisión partículas
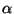 ,
, 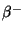 o captura electrónica (C.E.).
Después del decaimiento el
núcleo puede quedar en un estado excitado, es decir, con mayor energía de la
que necesita para encontrarse en su estado base. Esta energía extra es liberada
emitiendo rayos
o captura electrónica (C.E.).
Después del decaimiento el
núcleo puede quedar en un estado excitado, es decir, con mayor energía de la
que necesita para encontrarse en su estado base. Esta energía extra es liberada
emitiendo rayos 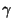 característicos del núcleo. La energía de estos rayos
característicos del núcleo. La energía de estos rayos
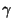 dependen de
los niveles energéticos internos que son diferentes para todos los
núcleos.
El nuevo núcleo producido por el decaimiento del anterior puede ser
también inestable y decaer a su vez en otro núcleo repitiendo todo el
proceso.
El comportamiento del núcleo se
estudia dentro del campo de la mecánica cuántica lo que impide
predecir el instante en el que un núcleo decae y solo es posible hablar en
términos de la probabilidad de decaimiento por intervalo de tiempo.
Si se considera que la probabilidad de que un núcleo decaiga por alguno de
los tipos de emisión ya mencionados en un intervalo de tiempo
dependen de
los niveles energéticos internos que son diferentes para todos los
núcleos.
El nuevo núcleo producido por el decaimiento del anterior puede ser
también inestable y decaer a su vez en otro núcleo repitiendo todo el
proceso.
El comportamiento del núcleo se
estudia dentro del campo de la mecánica cuántica lo que impide
predecir el instante en el que un núcleo decae y solo es posible hablar en
términos de la probabilidad de decaimiento por intervalo de tiempo.
Si se considera que la probabilidad de que un núcleo decaiga por alguno de
los tipos de emisión ya mencionados en un intervalo de tiempo 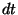 , ésta
es proporcional al intervalo de tiempo, esto es
, ésta
es proporcional al intervalo de tiempo, esto es 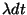 , donde
, donde
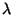 es la constante de decaimiento. Entonces se tiene que la
cantidad de núcleos inestables
es la constante de decaimiento. Entonces se tiene que la
cantidad de núcleos inestables 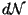 que decaen en un intervalo de tiempo
que decaen en un intervalo de tiempo
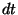 es:
es:
donde el signo negativo se introduce porque
el número de núcleos se irá reduciendo. Al resolver la ecuación diferencial
queda:
donde 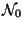 es el número inicial
de átomos. Esta ecuación es conocida como Ley de Decaimiento
Radiactivo.
También ha sido observado que la mayoría de núcleos pueden decaer por
tipos de emisión diferentes, es decir,
tienen cierta probabilidad de decaer por partículas
es el número inicial
de átomos. Esta ecuación es conocida como Ley de Decaimiento
Radiactivo.
También ha sido observado que la mayoría de núcleos pueden decaer por
tipos de emisión diferentes, es decir,
tienen cierta probabilidad de decaer por partículas 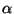 ,
cierta probabilidad de decaer por partículas
,
cierta probabilidad de decaer por partículas 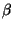 y cierta probabilidad de decaer por
C.E. Entonces la probabilidad de que este decaiga
en un intervalo
y cierta probabilidad de decaer por
C.E. Entonces la probabilidad de que este decaiga
en un intervalo 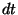 es
es
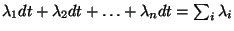 donde
donde 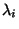 es la constante asociada
al tipo de decaimiento. Haciendo
es la constante asociada
al tipo de decaimiento. Haciendo
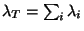 la ecuación
de decaimiento queda:
la ecuación
de decaimiento queda:
A partir de esta ecuación se pueden definir una serie de parámetros para describir
el comportamiento radiactivo:
Vida promedio 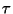 :
es el tiempo en el cual el número de átomo es igual a
:
es el tiempo en el cual el número de átomo es igual a 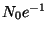 ,
es decir
,
es decir
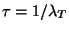 .
Vida media
.
Vida media 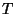 :
es el tiempo que tarda en reducirse el número de átomos a la mitad de su
número inicial; esto es:
:
es el tiempo que tarda en reducirse el número de átomos a la mitad de su
número inicial; esto es: 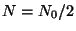 , lo cual da:
, lo cual da:
Probabilidad de emisión: este parámetro se refiere a la probabilidad de que
el núcleo decaiga por un tipo específico de emisión y está dado por:
La actividad: se define como el número de desintegraciones que ocurren por unidad
de tiempo, es decir:
donde 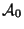 es la actividad inicial cuando existían
es la actividad inicial cuando existían 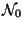 núcleos emisores.
Cuando el núcleo producto de la desintegración radiactiva es también inestable,
entonces se tiene una cadena y la existencia de los núcleos producto (hijos) dependen de
la actividad de los núcleos que los producen (padres) y el comportamiento se describe de la
siguiente forma:
núcleos emisores.
Cuando el núcleo producto de la desintegración radiactiva es también inestable,
entonces se tiene una cadena y la existencia de los núcleos producto (hijos) dependen de
la actividad de los núcleos que los producen (padres) y el comportamiento se describe de la
siguiente forma:
cuya solución es:
De las condiciones iniciales se tiene que:
al introducir estas condiciones en las ecuaciones diferenciales nuevamente se tiene:
y para el resto de coeficientes:
De esta forma, si se conocen las constantes de decaimiento para cada núcleo en
una cadena se puede estimar la cantidad de núcleos que habrán en un instante
dado.
Subsecciones




Next: Elementos radiactivos naturales
Up: tesis
Previous: INTRODUCCIÓN
Índice General
Hector Perez
2001-04-18