Distribución Maxwell-Boltzmann

Esta distribución se aplica al caso clásico, esto es, cuando las partículas se encuentran separadas distancias considerables y son distinguibles. Desde el punto de vista cuántico, las funciones de onda no se traslapan considerablemente.

$\begin{displaymath} n(E)=g(E)f(E) \end{displaymath}$

(3)

dónde

es el número de estados de energía

y corresponde al peso estadístico de la energía

$f(E)\,$ es la función de distribución y corresponde al número promedio de partículas en cada estado de energía

así como la probabilidad de ocupar cada estado de dicha energía. La función de distribución en términos de la temperatura absoluta es:

$\begin{displaymath} f_{MB}(E)=Ae^{\frac{-E}{kt}} \end{displaymath}$

(4)

$\begin{displaymath} n(E)=Ag(E)e^{\frac{-E}{kt}} \end{displaymath}$

(5)

Al aplicar estos resultados a un gas ideal, se considera que el número de moléculas es muy grande, y entonces la distribución de energías puede considerarse contínua. El término $n(E)dE\,\$ corresponde a las moléculas cuyas energías se encuentren entre

Para encontrar el factor de peso $g(E)\,$ es necesario conocer el número de estados con energías en el intervalo

y $E+dE.\,$ Al utilizar el espacio de momentum con $V=4\pi p^2dp,\,$ el número de estados de momentum estará dado por

$\begin{displaymath} g(p)dp=Bp^2dp \end{displaymath}$

(6)

Dado que cada magnitud de momentum corresponde a una energía determinada, el número de estados de energía

es el mismo para el número de estados de momentum

lo que permite no utilizar la función de partición

$\begin{displaymath} Z=\int\nolimits_0^\infty \frac{4\pi Vp^2dp}{h^3}e^{-\frac{\beta p^2}{2m}} \end{displaymath}$

(7)

para integrar en términos de momentum, sino utilizar la energía, $\beta$ corresponde al término $\frac 1{kt}$ y $p^2=2mE.\,$ Esta función es descrita en el capítulo 3, tal que

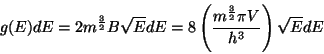$\begin{displaymath} g(E)dE=2m^{\frac 32}B\sqrt{E}dE=8\left( \frac{m^{\frac 32}\pi V}{h^3}\right) \sqrt{E}dE \end{displaymath}$

(8)

El número de moléculas con energías entre

y $E+dE\,$ será: $n(E)dE=C\sqrt{E}e^{-\beta E}dE,\,$ para encontrar la constante se utiliza la condición de normalización donde

$\begin{displaymath} N=\int_0^\infty n(E)dE \end{displaymath}$

(9)

$\begin{displaymath} N=\int_0^\infty n(E)dE=cN=\int_0^\infty \sqrt{E}e^{-\beta E}dE=\frac C2\sqrt{ \pi }(\beta )^{-\frac 32} \end{displaymath}$

(10)

$\begin{displaymath} C=\frac{2\pi N}{(\pi kT)^{3/2}}=2m^{\frac 32}A\left( \frac{4\pi V}{h^3} \right) \end{displaymath}$

(11)

$\begin{displaymath} n(E)dE=\frac{2\pi N}{(\pi kt)^{\frac 32}}\sqrt{E}e^{-\beta E}dE. \end{displaymath}$

(12)

Con estos datos es posible ahora calcular la energía total del sistema y luego encontrar la energía promedio por molécula:

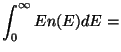$\displaystyle E$	$\textstyle =$	$\displaystyle \int_0^\infty En(E)dE=$	(13)
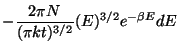	$\textstyle =$	$\displaystyle -\frac{2\pi N}{(\pi kt)^{3/2}}(E)^{3/2}e^{-\beta E}dE$
$\displaystyle E$	$\textstyle =$	$\displaystyle \frac 32NkT$

$\begin{displaymath} \bar{E}=\frac 32kT \end{displaymath}$

(14)

lo que es independiente de la masa de las moléculas. Esto corresponde solamente a la energía traslacional del estado

de las moléculas.