Criterio de validez del regimen clásico

Para la distribución de Maxwell Boltzmann se especificaba que la mayoría de los estados de partículas simples esten vacíos y pocos contengan una molécula y es mucho menor donde hay más de una molécula.

Partiendo de la probabilidad de que una molécula esté en un estado de energía cinética dada de acuerdo a la distribución es:

$$p_r=\frac 1Ze^{-\beta E}$$ (15)

donde $Z$ corresponde a y $p_r=\left( \frac{e^{-\beta E}}{ V\left( \frac{2\pi mkT}{h^2}\right) ^{\frac 32}}\right)$

donde obtenemos que el número promedio de moléculas que se encuentran en el estado traslacional $s$ con momentum respectivo $p_s$

$$\overline{n}=Np_s=\frac NV\left( \frac{h^2}{2\pi mkT}\right) e^{-\beta E}$$ (16)

la condición clásica se cumple si $\overline{n}$ es muy pequeño $(\overline{n}\ll 1)$ porque así los estados se encuentran en mayoría desocupados o con una molécula lo más. Esta condición se transforma en:

$$\frac NV\left( \frac{h^2}{2\pi mkT}\right) ^{\frac 32}\ll 1$$ (17)

condición suficiente para la validez del régimen. También es claro que a temperaturas altas (Kelvin) y bajas densidades la distribución se ajusta mejor, de manera que la del gas ideal se mantiene. Para interpretar la condición del régimen clásico es necesario recurrir a ciertos conceptos de mecánica cuántica. Partiendo de que una partícula tiene un momentum $p$ asociado con la longitud de onda de de Broglie

$$\lambda _{dB}=\frac hp=\frac h{\sqrt{\left( 2mE\right) }}$$ (18)

recordando el resultado obtenido para energía cinética media de las partículas $\overline{E}=\frac 32kT$

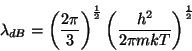$$\lambda _{dB}=\left( \frac{2\pi }3\right) ^{\frac 12}\left( \frac{h^2}{2\pi mkT}\right) ^{\frac 12}$$ (19)

donde es claro que la introducción del factor $2\pi$ obedece a la conveniencia de escribirlo así para encontrar el factor de , sustituyendo este resultado en dicha ecuación encontramos que:

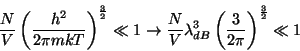$$\frac NV\left( \frac{h^2}{2\pi mkT}\right) ^{\frac 32}\ll 1\... ...NV\lambda _{dB}^3\left( \frac 3{2\pi }\right) ^{\frac 32}\ll 1$$ (20)

y recordando que la distancia media entre moléculas es $l=\left( \frac VN\right) ^{\frac 13}$ y nuevamente haciendo las sustituciones del caso

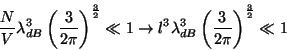$$\frac NV\lambda _{dB}^3\left( \frac 3{2\pi }\right) ^{\frac ... ...^3\lambda _{dB}^3\left( \frac 3{2\pi }\right) ^{\frac 32}\ll 1$$ (21)

en esta relación el factor $\left( \frac 3{2\pi }\right) ^{\frac 32}$ es una constante por tanto la relación entre las variables es

$$\lambda _{dB}^3\ll l^3$$ (22)

que reformulando la condición en se establece que la longitud de onda de de Broglie debe ser pequeña comparada con la separación entre moléculas. Esto es evidente para evitar los efectos de interferencia entre las ondas de de Broglie para distintas partículas. Esto concuerda con la derivación para la distribución de Maxwell Boltzmann (caso clásico) donde las partícualas obedecen la mecánica Newtoniana. Sin embargo, cuando $\lambda _{dB}^3$ es comparable con $l^3$ estos efectos son apreciables la distribución no describe el fenómeno de manera aceptable y es necesario utilizar la mecánica cuántica.