Cualquier transición que ocurra donde exista un cambio de entropía y
volumen y además, las derivadas de primer orden del potencial de Gibbs
presentan discontinuidades se denomina de primer orden. Es
necesario recalcar que durante la transición de fase ![]() se hace
infinito, durante una transición de primer orden únicamente; ya que
no hay cambios de presión ni temperatura.
se hace
infinito, durante una transición de primer orden únicamente; ya que
no hay cambios de presión ni temperatura.
Si se considera una mezcla de gas-líquido en equilibrio, la cual
representa un caso de transición de orden cero, a una temperatura ![]() y
presión de vapor
y
presión de vapor ![]() conociendo que la masa de líquido sea
conociendo que la masa de líquido sea ![]() y la masa de gas sea
y la masa de gas sea ![]() , cuando ocurre la transición, el
potencial de Gibbs debe estar en un mínimo para este estado
, cuando ocurre la transición, el
potencial de Gibbs debe estar en un mínimo para este estado ![]() . Esto indica un proceso reversible a temperatura y presión
constantes. [13, 210]
. Esto indica un proceso reversible a temperatura y presión
constantes. [13, 210]
Utilizando la notación donde los superíndices indican el estado al
que se refiere, siendo ![]() y
y ![]() inicial y final, respectivamente. Se
denomina
inicial y final, respectivamente. Se
denomina ![]() al potencial de Gibbs por unidad de masa; para comprobar la
suposición anterior se consideran dos transiciones. Una transición
de un estado inicial a
al potencial de Gibbs por unidad de masa; para comprobar la
suposición anterior se consideran dos transiciones. Una transición
de un estado inicial a ![]() y uno final a
y uno final a ![]() donde se
cumple
donde se
cumple
| (29) |
| (30) |
restando ambas ecuaciones es posible encontrar la variación de ![]() que
denominaremos de orden 0
que
denominaremos de orden 0
| (31) |
reescribiendo explícitamente en términos de ![]() y
y ![]()
Esta expresión es equivalente a
cuando se consideran dos puntos sobre el diagrama de fase y por tanto dos
estados ![]() y
y ![]() que sufren una transición de un estado inicial a
un estado final.
que sufren una transición de un estado inicial a
un estado final.
Utilizando la definición del calor latente de transición ![]()
![]() y
y ![]()
Esta relación es conocida como la ecuación de Clapeyron. Los cambios
de fase se caracterizan por una discontinuidad en ![]() . Las
discontinuidades mencionadas también pueden conllevar a cambios de
entropía y volumen molar. La diferencia en la entropía involucra un
calor latente de transición. Este tipo de transición se denominada
de primer orden. Transiciones de primer orden son ejemplificadas
con transiciones como las de sólido-líquido o las transiciones
alotrópicas ( sarros de gris a blanco, nanotubos).
. Las
discontinuidades mencionadas también pueden conllevar a cambios de
entropía y volumen molar. La diferencia en la entropía involucra un
calor latente de transición. Este tipo de transición se denominada
de primer orden. Transiciones de primer orden son ejemplificadas
con transiciones como las de sólido-líquido o las transiciones
alotrópicas ( sarros de gris a blanco, nanotubos).
Es posible hacer varias deducciones a partir de la ecuación de Clapeyron (también llamada Classius-Clapeyron)[23, 228] como por ejemplo: la fusión, la evaporación y la sublimación. Los cambios en la entropía y por lo tanto los cambios en el calor latente son positivos. El carácter positivo de estos cambios es consecuencia directa de que son cambios ordenados del sistema. Para transiciones de sólido a líquido y a gas la densidad decrece y el cambio de volumen es positivo, tal que el volumen molar se incrementa. Esto corresponde a que una sustancia se expande o contrae dependiendo de si es un proceso de fusión o de sublimación. Esta relación se cumple en todas las transiciones de primer orden para la presión de vapor. Es fácilmente comprobable que se cumple en estas transiciones si conocemos que
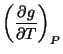 |
(35) | ||
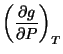 |
(36) |
y comprobamos que las primeras derivadas de los potenciales
químicos no son iguales,
![]() se cumple que la
transición es de primer orden.
se cumple que la
transición es de primer orden.
Si las primeras derivadas son continuas en el punto de transición la
ecuación de Clapeyron no es válida y no es una transición de
primer orden. Esto se refleja en el diagrama ![]() donde las isotermas no
presentarán un comportamiento horizontal. Ehrenfest [13, 35],
define el orden de las transiciones de fase de acuerdo con
donde las isotermas no
presentarán un comportamiento horizontal. Ehrenfest [13, 35],
define el orden de las transiciones de fase de acuerdo con
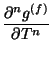 |
(37) | ||
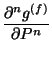 |
(38) |
donde ![]() corresponde al orden de la transición ya que se establece la
condición de que las derivadas de orden
corresponde al orden de la transición ya que se establece la
condición de que las derivadas de orden ![]() sean continuas. Un
ejemplo conocido de una transición de segundo orden es la
superconductividad.
sean continuas. Un
ejemplo conocido de una transición de segundo orden es la
superconductividad.