Teoría de Yang y Lee

En 1952 Chen Ning Yang y Tsung Dao Lee publican su teoría sobre las transiciones de fase. Ejemplifican la teoría con la descripción de la condensación y el modelo Ising. Ellos toman modelos conocidos como el de Mayer y lo completan. El modelo mencionado no explicaba por qué las isotermas en una transición permanecen horizontales.

Utilizan la función de macro partición descrita más adelante en este informe. Resolvieron el problema enfocándolo desde otro punto de vista. Dejan que la fugacidad tome valores complejos, de tal manera que la función de macro partición se refiere a un ensemble de átomos interactuando.

La prueba completa de su teoría se puede encontrar en los artículos originales.[29, 404] Muestran que el problema puede solucionarse si las transiciones de fase son gobernadas por la distribución de las raíces de la función de partición en el plano complejo $z$. ``La transición ocurre cuando una raíz se aproxima al eje real en el límite donde $V\rightarrow 0''$. [13, 208]

Si se considera un gas de volumen finito, las moléculas tienen un volumen definido. Pero cuando hay contacto entre ellas, (al interactuar) los términos de la función de partición desaparecen y el potencial cambia. Esto lleva a que la energía de interacción sea infinita. La razón para tomar estos límites es que en mecánica estadística es posible encontrar el valor medio de $\rho$ por medio de la función de partición. Sin embargo, en termodinámica se considera una muestra infinita y las funciones termodinámicas son límites de los valores medios, cuando el volumen se hace infinito.

Esto puede resumirse en dos teoremas:[13, 208]

TEOREMA 1

Para todos los valores de $z>0$,

$$F_\infty (z)\equiv V^{-1}\log \mathcal{Z}_v(z,V)$$

se aproxima al límite donde es independiente de la forma de $V$, cuando $V\rightarrow \infty .$ Este límite es una función de $z$ que se incrementa monótonamente si y solo si $V$ no se incrementa más rápido que $V^{\frac 23}.$

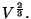
TEOREMA 2

Si en el plano complejo $z$ se considera una región $R,$ que contiene un segmento del eje real positivo y no contiene raíces de la función de macro partición. En esta región la cantidad $V^{-1}\log \mathcal{Z} _v\,$ converge uniformemente a medida que $V\rightarrow \infty .\,$ El límite es analítico para todo $z$ en la región $R.$

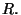
Al utilizar la forma paramétrica de ecuación de estado y los teoremas anteriores

$$\rho =\lim\limits_{V\rightarrow \infty }\frac \partial {\partial \log z}\frac 1V\log \mathcal{Z}_v$$ (39)

Esta cantidad no siempre es analítica. Esto es: la densidad no asume un valor definido en la condensación. Se concluye que en una región donde no existen raíces de $z,$ la ecuación de estado exhibe el comportamiento de una sola fase. En el caso de encontrar raíces de la función de macro partición se observarán dos regiones. Cada región libre de ceros de la función.

En un punto de la transición se cumple que $P$ debe ser continua y su derivada puede ser discontinua. Es necesario notar que la transición ocurre solo en el eje positivo de $z$, en el cual las raíces de la ecuación $\mathcal{Z}_v(z)=0,$ convergen a medida de que el volumen se hace infinito.