Condensación Bose-Einstein

Las propiedades de estos condensados incluyen superfluidez (en ausencia de viscosidad) y en estado líquido no interactúa con líquidos viscosos, tiene una entropía cero y presenta comportamientos característicos en el calor específico. La transición es acompañada de un comportamiento peculiar en el calor específico, el punto donde ocurre esto es precisamente $T_{c.}$ Llamado punto $\lambda .$ Experimentalmente, para helio líquido esto corresponde a 2.17K, sin embargo la teoría tiene algunas fallas porque asume un gas ideal donde las interacciones entre átomos son despreciables. Sin embargo para bosones (spin entero) esto es válido. Helio 3 presenta superfluidez pero en 3 órdenes de magnitud menores, esto se debe a que los átomos presentan spin $\frac 12.$

Conociendo la distribución Bose Einstein y la fugacidad conduce a

$$\frac Sk=\sum\limits_ig_i\left[ \frac{\beta \mathcal{E}_i-\l... ...ta \mathcal{E}_i}+1}-\log (1-ze^{-\beta \mathcal{E}_i})\right]$$ (106)

donde se hace necesario introducir dos definiciones

$$\lambda =\sqrt{\frac{2\pi h^2}{mkT}}$$ (107)

que corresponde a la longitud de onda térmica (del orden de magnitud de la longitud de onda de De Broglie de una partícula de masa $m$ y energía $kT),$ y el volumen específico $v=V/N.$ Se reescribe la fugacidad como

$$z=\frac{\lambda ^3}v$$ (108)

y de la función de partición:

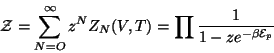$$\mathcal{Z}=\sum\limits_{N=O}^\infty z^NZ_N(V,T)=\prod \frac 1{1-ze^{-\beta \mathcal{E}_p}}$$ (109)

se rescribe la ecuación de estado como:

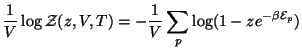$$\frac P{kT} = \frac 1V\log \mathcal{Z}(z,V,T)=-\frac 1V\sum\limits_p\log (1-ze^{-\beta \mathcal{E}_p})$$ (110)

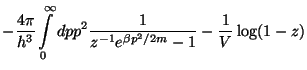$$= -\frac{4\pi }{h^3}\int\limits_0^\infty dpp^2\frac 1{z^{-1}e^{\beta p^2/2m}-1}-\frac 1V\log (1-z)$$ (111)

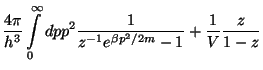$$\frac 1v = \frac{4\pi }{h^3}\int\limits_0^\infty dpp^2\frac 1{z^{-1}e^{\beta p^2/2m}-1}+\frac 1V\frac z{1-z}$$ (112)

de donde es posible con las sustituciones de la fórmula de Stirling para valuar las integrales que:

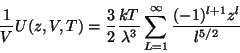$$\frac 1VU(z,V,T)=\frac 32\frac{kT}{\lambda ^3}\sum\limits_{L=1}^\infty \frac{ (-1)^{l+1}z^l}{l^{5/2}}$$ (113)

Si se asume que a pesar de que el término $p=0$ es significativo, es posible despreciarlo tal que despreciamos $V^{-1}(\log (1-z)).$ Esto y la eliminación de $z$ de la ecuación anterior nos llevan a escribir $U$ como función únicamente $V,T$ y $N.$ Esto lleva a una función muy complicada debido a la dependencia de $z$ con $T.$

Al comparar las ecuaciones anteriores se concluye que la energía $U$ debe ser relacionada directamente con la presión tal que:

$$U=\frac 32PV$$ (114)

relación que es válida para los gases ideales descritos por cualquiera de las distribuciones estadísticas (Boltzmann, Bose-Einstein, Fermi-Dirac).

Al rescribir el número medio de estados ocupados $\left\langle n_p\right\rangle$ en función de la fugacidad

$$\left\langle n_p\right\rangle =\frac{ze^{-\beta \mathcal{E}_p}}{1\mp ze^{-\beta \mathcal{E}_p}}$$ (115)

cumpliendo que $N=\sum\limits_p\left\langle n_p\right\rangle .$ Este resultado nos indica que la fracción $\left( \frac z{1-z}\right)$ corresponde al nivel $p=0.$

Esto es significativo cuando son los estados más bajos los más ocupados como en el caso que nos interesa que es la condensación Bose-Einstein.

Regresando a la ecuación de estado, al encontrar la fugacidad como función de $T$ y $v$ al resolver

$$\frac 1v=\frac 1{\lambda ^3}g_{3/2}(z)+\frac 1V\frac z{1-z}$$ (116)

con $v=V/N,$ y $\lambda =\sqrt{2\pi \hbar ^2/mkT}.$ Se conoce que $g_{3/2}(z)$ pertenece a un grupo de funciones especiales (no confundir con el factor de peso introducido para la deducción de la distribución estadística Bose-Einstein), $n$ corresponde al número de la función especial

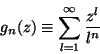$$g_n(z)\equiv \sum\limits_{l=1}^\infty \frac{z^l}{l^n}$$ (117)

entre $0$ y $1$ la función $z$ se encuentra acotada, es positiva y continua. La solución gráfica de esta función se muestra en las figuras 1 y 2. Para satisfacer la ecuación de estado es necesaria la condición

$$0\leq z\leq 1$$ (118)

para valores pequeños de $z$ es válido aproximar a la función $g_{3/2}(z)$ como una serie de potencias:

$$g_{3/2}(z)=z+\frac{z^2}{2^{3/2}}+\frac{z^3}{3^{3/2}}+...$$ (119)

para $z=1,$ la derivada diverge pero tiene un valor definido

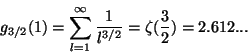$$g_{3/2}(1)=\sum\limits_{l=1}^\infty \frac 1{l^{3/2}}=\zeta (\frac 32)=2.612...$$ (120)

siendo $\zeta (\frac 32)$ la función zeta de Riemann. Esto acota el intervalo de $z,$ de manera que para todo $z$ entre $0$ y $1$ debe ser $\leq 2.612...$, tal y como se ve de la Figura 3.

Con estas consideraciones al reescribir la ecuación de estado:

$$\lambda ^3\frac{\left\langle n_0\right\rangle }V=\frac{\lambda ^3} v-g_{3/2}(z)$$ (121)

que es positiva la fracción $\left\langle n_0\right\rangle /V$ si las condiciones son tales que

$$\frac{\lambda ^3}v>g_{3/2}(1)$$ (122)

Figure: $g_{3/2}$ [13]

Esto describe que la fracción de partículas que ocupa el nivel con $p=0$ es finita y el fenómeno de la condensación Bose-Einstein por esto es a veces descrito como una condensación en el espacio de momentum. Corresponde en un subespacio termodinámico $P-v-T$ del gas ideal de bosones a la región donde ocurre la transición de una fase a otra. Esta región se considera como una mezcla de partículas con $p=0$ y partículas con $p\neq 0,$ que es donde ocurre la condensación. $\cite[188]{huang}$

Se define la superficie de separación de ambos estados como $\frac{ \lambda ^3}v=g_{3/2}(1)$ y la temperatura crítica luego de sustituir el factor $\lambda$

$$kT_c=\frac{2\pi \hbar ^2/m}{\left[ vg_{3/2}(1)\right] ^{2/3}}$$ (123)

Figure: Solución gráfica [13]

$T_c$ corresponde la longitud de onda térmica donde es comparable con la separación promedio entre partículas. Esto conduce a definir un volumen crítico como:

$$v_c=\frac{\lambda ^3}{g_{3/2}(1)}$$ (124)

Figure: Fugacidad [13]

Se justifica que la transición sea de primer orden porque al encontrar el calor latente de transición por partícula, utilizando la Ec. de Clapeyron

$$l=\frac{g_{5/2}(1)}{g_{3/2}(1)}\frac 52kT$$ (125)

utilizando las funciones termodinámicas, con estos nuevos parámetros, y reescribiendo la región de transición de forma que

$$\frac SN=\left( \frac T{T_c}\right) ^{3/2},s=\left( \frac v{v_c}\right) s$$ (126)

se encuentra que

$$s=\frac{g_{5/2}(1)}{g_{3/2}(1)}\frac 52k$$ (127)

sabiendo que $S$ corresponde a la entropía total, $s$ es reconocido como la entropía por partícula en la fase gaseosa. Al comparar estas ecuaciones es posible encontrar que el calor latente de transición

$$l=T\Delta s$$ (128)

que concuerda con nuestra definición de transiciones de primer orden del capítulo 2.

Finalmente es necesario recalcar que los condensados ocurren solamente cuando se conserva el número de partículas. Ahora los fullerenes son una forma de condensados, ya que son producidos bajo las mismas condiciones. Tienen los mismos requerimientos sobre la función de onda y tienen los mismos parámetros termodinámicos.