



Next: APLICACIÓN DEL FORMALISMO ADM
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Formulación hamiltoniana
Índice General
Al considerar las fuentes del campo gravitacional, es decir, la materia; las
ecuaciones de Einstein son
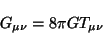 |
(3.27) |
esta ecuación es la forma covariante de la ec. 2.38. La
parte izquierda de la ec. 3.27 se construyó
exclusivamene de cantidades que involucran a la geometría del
espacio-tiempo. La parte derecha representa la fuente del campo
gravitacional.
En esta sección se obtendrá la densidad lagrangiana para campos de
materia por medio del tensor de momento y energía 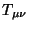 , y con
la suposición de que esta densidad lagrangiana
, y con
la suposición de que esta densidad lagrangiana
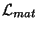 no
contiene derivadas de la métrica; así, las variaciones de
no
contiene derivadas de la métrica; así, las variaciones de
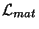 con respecto al tensor métrico
con respecto al tensor métrico 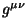 son dadas por
derivadas parciales con respecto a la métrica. En otras palabras, el
conjunto de ecuaciones diferenciales que debe satisfacer la densidad
lagrangiana de materia
son dadas por
derivadas parciales con respecto a la métrica. En otras palabras, el
conjunto de ecuaciones diferenciales que debe satisfacer la densidad
lagrangiana de materia
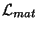 están dadas por la siguiente
relación
están dadas por la siguiente
relación
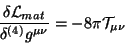 |
(3.28) |
donde
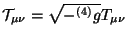 nos representa
la densidad tensorial de
nos representa
la densidad tensorial de 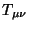 . De este modo, se puede escribir
estas derivadas parciales
. De este modo, se puede escribir
estas derivadas parciales
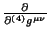 en términos de
en términos de
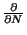 ,
,
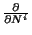 y
y
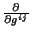 , y así construir un
conjunto de ecuaciones diferenciales parciales para
, y así construir un
conjunto de ecuaciones diferenciales parciales para
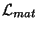 ,
dependiendo únicamente de las variables
,
dependiendo únicamente de las variables
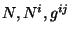 , y de los campos
de materia que se contemplan en el tensor
, y de los campos
de materia que se contemplan en el tensor 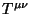 .
La métrica contravariante
.
La métrica contravariante
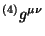 en términos de las
variables ADM se expresa en la ec. 3.14 de donde se puede
evaluar directamente las correspondientes derivadas parciales, como se
observa a continuación [10]
en términos de las
variables ADM se expresa en la ec. 3.14 de donde se puede
evaluar directamente las correspondientes derivadas parciales, como se
observa a continuación [10]
Los otros términos vienen a ser
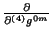 ,
,
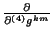
Usando la ec. 3.28, se puede escribir las expresiones
correspondientes a las ecs. 3.29, 3.30 y 3.31, quedando de la
siguiente manera




Next: APLICACIÓN DEL FORMALISMO ADM
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Formulación hamiltoniana
Índice General
enrique pazos
2000-09-27