| (208) |
The free Lagrangian for ``nucleons" (considered as point particles)
reads:
| (209) |
| (210) |
``...It seems that this is not consistent with the concept of the localized field which supports the usual physical theories. In the present work we want to explore the possibility of requiring all interactions to be invariant under isotopic spin rotations which are independent in each point of the space-time".
What happens then if different isotopic transformations are
implemented in different points of the space-time? That is to say,
what is the consequence of a local isotopic phase transformation with
Certainly, the mass term of ![]() , does not represent any problem,
as it was the case in
, does not represent any problem,
as it was the case in ![]() because it is invariant even when the
freedom (213) is choosen. Nevertheless, for the term with derivative
one has
because it is invariant even when the
freedom (213) is choosen. Nevertheless, for the term with derivative
one has
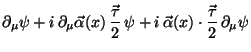 |
(212) | ||
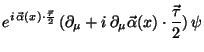 |
(213) |
| (214) |
It is an isovector field which is added to the derivative in ![]() so
that the covariant derivative is defined
so
that the covariant derivative is defined
| (215) |
Then, it results
Again the requirement of local invariance determines the
interaction. Certainly, the gauge invariance of second class of the
Lagrangian imposes a precise transformation law for the gauge field
![]() . If
. If ![]() is supposed invariant, we can write
is supposed invariant, we can write
![$\displaystyle \bar{\psi}' [i \gamma^{\mu} (\partial_{\mu} - i g \vec{b}'_{\mu} \cdot\frac{\vec{\tau}}{2}) - m] \psi'$](img484.gif) |
(217) | ||
![$\displaystyle \bar{\psi} e^{-i \vec{\alpha}\cdot\frac{\vec{\tau}}{2}} [i \g...
...ot\frac{\vec{\tau}}{2}) -m] e^{i \vec{\alpha}\cdot\frac{\vec{\tau}}{2}} \psi$](img485.gif) |
(218) | ||
![$\displaystyle \bar{\psi} [i \gamma^{\mu} (\partial_{\mu} - i g\vec{b}_{\mu}\cdot\frac{\vec{\tau}}{2}) - m] \psi$](img486.gif) |
(219) |
| (220) |
| (221) |
But remembering (186) the transformation law of the Yang-Mills field
emerges
In conclusion, the Lagrangian (218) is invariant under local isospin phase transformations - transformations (209) with (213) - if the gauge field is simultaneously transformed as (224).
Once the Yang-Mills field is introduced in the game, it is clear that
the complete description of the theory implies establishing the free
Lagrangian of the gauge field. For the electromagnetic case it is
known that
| (223) |
| (224) |
For the case of isotopic invariance ![]() will be,
as usual, a function of the field
will be,
as usual, a function of the field ![]() and of its derivatives.
The different fact is that in order to satisfy local invariance, there
must appear in the more involved combination
and of its derivatives.
The different fact is that in order to satisfy local invariance, there
must appear in the more involved combination
| (226) |
Summarizing, the local ![]() invariant Lagrangian for the field
of the ``nucleon" is
invariant Lagrangian for the field
of the ``nucleon" is
| (227) |