



Next: Identidades de Bianchi
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Derivada covariante
Índice General
El tensor de Riemann se obtiene de la siguiente expresión
![\begin{displaymath}
\left[ \nabla _{\nu },\nabla _{\mu }\right] A_{\beta %%
}\equiv R_{\beta \mu \nu }^{\alpha }A_{\alpha }
\end{displaymath}](img247.gif) |
(2.27) |
donde
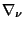 es la derivada covariante respecto de
es la derivada covariante respecto de 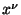 y
y
![$\left[ \nabla _{\nu },\nabla _{\mu }\right] $](img250.gif)
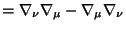 . El tensor de Riemann
. El tensor de Riemann
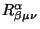 se puede interpretar como una medida de la no conmutatividad de la derivada
covariante. Este tensor puede ser obtenido a partir de los símbolos de
Christoffel y sus derivadas [5]
se puede interpretar como una medida de la no conmutatividad de la derivada
covariante. Este tensor puede ser obtenido a partir de los símbolos de
Christoffel y sus derivadas [5]
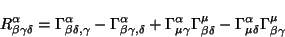 |
(2.28) |
Al bajar el índice contravariante del tensor de Riemann se obtiene el
tensor de curvatura, dado como
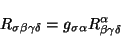 |
(2.29) |
El tensor de Riemann tiene 256 componentes pero no todas son independientes
debido a las simetrías que presenta este tensor. Algunas de ellas son
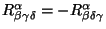 y
y
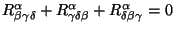 El tensor de Ricci de encuentra contrayendo en tensor de Riemann de la
siguiente manera
El tensor de Ricci de encuentra contrayendo en tensor de Riemann de la
siguiente manera
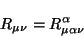 |
(2.30) |
La elección del índice covariante a contraer no es fija. En este
trabajo se toma la definición dada en la ecuación anterior. [5]
Otra forma de expresar la curvatura del espacio-tiempo es mediante el
escalar de curvatura, que es
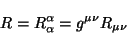 |
(2.31) |
en donde 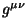 es el tensor métrico contravariante y satisface
la relación
es el tensor métrico contravariante y satisface
la relación
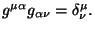




Next: Identidades de Bianchi
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Derivada covariante
Índice General
enrique pazos
2000-09-27