



Next: Tensor de momentum y
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Tensor de Riemann, tensor
Índice General
El principio, Einstein supuso que el tensor de Ricci se debía igualar
al tensor de materia; de esta manera la materia sería la fuente de la
gravedad. Esto no funcionó ya que la divergencia del tensor de materia
se hace cero y la del tensor de Ricci no siempre lo es. Para encontrar un
tensor que cumpliera con la condición anterior se recurre a las identidades de Bianchi, que son satisfechas por la derivada covariante del
tensor de curvatura
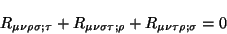 |
(2.32) |
Estas identidades forman un conjunto de 1024 ecuaciones de la cuales la
mayoría no dice nada. Esencialmente son 24 identidades que no son
triviales. Multiplicando la ec. 2.32 por
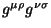 y usando la difinición del tensor de Ricci y de escalar de
curvatura, junto con las propiedades de simetría del tensor de Riemann
se llega a que [6]
y usando la difinición del tensor de Ricci y de escalar de
curvatura, junto con las propiedades de simetría del tensor de Riemann
se llega a que [6]
lo cual define el tensor de Einstein
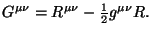 Por igualdad, este tensor satisface la
condición de divergencia
Por igualdad, este tensor satisface la
condición de divergencia
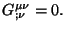




Next: Tensor de momentum y
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Tensor de Riemann, tensor
Índice General
enrique pazos
2000-09-27