



Next:FORMALISMO
ADM EN RELATIVIDADUp:DE
LA RELATIVIDAD ESPECIALPrevious:Identidades
de BianchiÍndice
General
Tensor de momentum y energía
El postulado de Einstein para el espacio vacío establece que
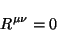 |
(2.34) |
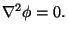 Cuando se considera una distribución de carga la ecuación
de Laplace se convierte en la ecuación de Poisson,
Cuando se considera una distribución de carga la ecuación
de Laplace se convierte en la ecuación de Poisson, 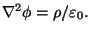 Además, la carga cumple con la ecuación de continuidad dada
por [7]
Además, la carga cumple con la ecuación de continuidad dada
por [7]
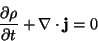 |
(2.35) |
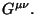 Por analogía con la electrostática, se postula que
Por analogía con la electrostática, se postula que
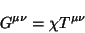 |
(2.36) |
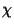 es una constante y
es una constante y 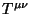 es el tensor de momentum y energía. En la sección
anterior se vio que el tensor de Einstein cumple que
es el tensor de momentum y energía. En la sección
anterior se vio que el tensor de Einstein cumple que 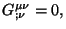 por lo tanto, el tensor de momentum y energía también
cumple la misma propiedad, es decir,
por lo tanto, el tensor de momentum y energía también
cumple la misma propiedad, es decir,
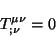 |
(2.37) |
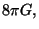 donde
donde 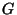 es la constante de gravitación universal; se obtiene
es la constante de gravitación universal; se obtiene
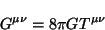 |
(2.38) |
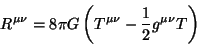 |
(2.39) |
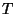 es la traza del tensor de energía-momentum y es igual a
es la traza del tensor de energía-momentum y es igual a 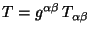 .
.




Next:FORMALISMO
ADM EN RELATIVIDADUp:DE
LA RELATIVIDAD ESPECIALPrevious:Identidades
de BianchiÍndice
General
enrique pazos 2000-09-27