Principio variacional

Habiendo definido un nuevo conjunto de variables, se puede ahora reescribir el elemento de volumen y el escalar de curvatura con el fin de reformular la acción para el campo gravitacional, la cual está dada por la ec. 3.2. En términos de las variables ADM la acción queda de la forma

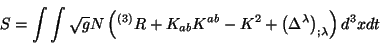$$S=\int \int \sqrt{g}N\left( ^{\left( 3\right) }R+K_{ab}K^{a... ...eft( \Delta ^{\lambda }\right) _{;\lambda }\right) d^{3}xdt$$ (3.15)

En esta ecuación se puede ver que el elemento de volumen queda ahora como

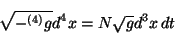$$\sqrt{-^{(4)}g}d^{4}x=N\sqrt{g}d^{3}x\,dt$$ (3.16)

y que el escalar de curvatura queda expresado en función del escalar de curvatura en tres dimensiones 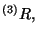$^{( 3)}R,$ la curvatura extrínseca 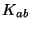$%% K_{ab}$ y una divergencia designada por $\left( \Delta ^{\lambda }\right) _{;\lambda }.$

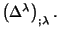
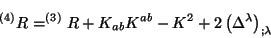$$^{\left( 4\right) }R= ^{\left( 3\right) }R+K_{ab}K^{ab}-K^{2}+2\left( \Delta ^{\lambda }\right) _{;\lambda }$$ (3.17)

El cálculo detallado de estas cantidades es tratado en la referencia [9]. Es importante hacer notar el hecho de que no solamente la expresión para el lagrangiano se ha modificado, sino también hay que hacer una nueva interpretación de la acción. En la ec. 3.2 la integral es sobre todo el expacio tiempo. Esto implica que cuando se hace la variación, los términos que están evaluados en la frontera se cancelan, ya que se pide que la variación de la métrica y sus derivadas sea cero en la frontera (métrica asintóticamente minkowskiana). En la ec. 3.15 la interpretación es diferente puesto que se tienen dos integrales diferentes. La primera integral es sobre la hipersuperficie, es decir, que el lagrangiano está dado por una integral sobre la hipersuperficie de la forma

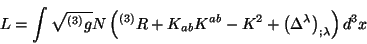$$L=\int \sqrt{^{\left( 3\right) }g}N\left( ^{\left( 3\right)... ...}-K^2+\left( \Delta ^\lambda \right) _{;\lambda }\right) d^3x$$ (3.18)

por lo que la acción está dada por una integral del lagrangiano entre un tiempo inicial y un tiempo final

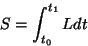$$S=\int_{t_0}^{t_1}Ldt$$ (3.19)

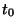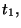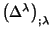Esto quiere decir que se está especificando la métrica sobre la hipersuperficie inicial $t_0$ y sobre la final $t_1,$ por lo que la variación será sobre todas la hipersuperficies que conecten a las dos hipersuperficies de los extremos. La divergencia $\left( \Delta ^\lambda \right) _{;\lambda }$ que aparece en la integral se transforma en una integral sobre la frontera de la hipersuperficie. Estos términos no aportan información dinámica alguna y por lo tanto pueden despreciarse. [9]