



Next: Lagrangiano de los campos
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Principio variacional
Índice General
Hasta ahora se ha obtenido la acción gravitacional de tal manera que al
hacer la variación de la misma e igualarla a cero se llega a las
ecuaciones de campo en el vacío. Este procedimiento conduce a la
obtención de ecuaciones diferenciales de segundo orden. Si lo que se
quiere es tener ecuaciones de primer orden, existen varias formas de
lograrlo. Uno de ellos es tomar la acción à la Palatini. [5] El otro camino consiste en definir nuevas variables, los momentos,
a partir del lagrangiano; luego tratar de reescribir el lagrangiano en
términos de las variables originales y los momentos, tomándolas como
variables independientes. Esto duplica el número de variables
independientes e involucra la construcción de un hamiltoniano.
Para esto se definen los momentos canónicamente conjugados a las seis
componentes 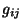 de la forma siguiente
de la forma siguiente
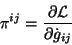 |
(3.20) |
Los momentos asociados a las variables 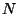 y
y 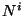 serán iguales a cero
puesto que la densidad lagrangiana no depende de sus derivadas temporales.
El hamiltoniano estará dado por
serán iguales a cero
puesto que la densidad lagrangiana no depende de sus derivadas temporales.
El hamiltoniano estará dado por
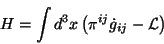 |
(3.21) |
en función de las variables ADM, esta expresión se convierte en
donde
la barra ''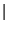 '' representa la derivada covariante en tres dimensiones.
Ahora se puede escribir el lagrangiano a partir de las ecs. 3.21 y 3.22
'' representa la derivada covariante en tres dimensiones.
Ahora se puede escribir el lagrangiano a partir de las ecs. 3.21 y 3.22
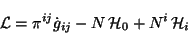 |
(3.25) |
La ec. 3.23 se puede escribir en función de los momentos 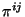 de la siguiente manera
de la siguiente manera
![\begin{displaymath}
\mathcal{H}_{0}=-\sqrt{^{\left( 3\right) }g}\left[ ^{\left(...
...( \pi _{k}^{k}\right)
^{2}-\pi ^{ij}\pi _{ij}\right) \right]
\end{displaymath}](img348.gif) |
(3.26) |




Next: Lagrangiano de los campos
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Principio variacional
Índice General
enrique pazos
2000-09-27