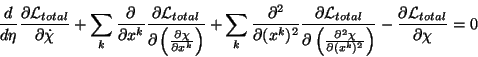Next: Buscando la solución general
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Ecuaciones de Einstein
Índice General
Cuando se requiere obtener la información sobre que tipo de variables
están involucradas en un problema de lagrangianos, se necesita obtener esa
información directamente del problema mismo. Siendo esto así, se
puede ver que las variables independientes para este problema en particular
son 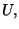
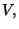
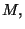
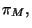
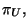
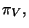
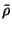 y
y 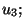 ya que al ser consideradas como tales, se debe hacer la variación
de la densidad lagrangina sobre estas variables, las cuales deben conducir a
combinaciones de las ecuaciones de Einstein obtenidas anteriormente.
Del análisis de la densidad lagrangiana, se observa que se trata con un
objeto del tipo
ya que al ser consideradas como tales, se debe hacer la variación
de la densidad lagrangina sobre estas variables, las cuales deben conducir a
combinaciones de las ecuaciones de Einstein obtenidas anteriormente.
Del análisis de la densidad lagrangiana, se observa que se trata con un
objeto del tipo
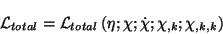 |
(4.38) |
donde
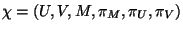 , representa a todas las variables
sobre las cuales se variará la densidad lagrangiana. Se puede observar
que
, representa a todas las variables
sobre las cuales se variará la densidad lagrangiana. Se puede observar
que
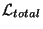 depende de las segundas derivadas de las
coordenadas, por lo tanto la ecuación de Euler-Lagrange para sistemas
continuos esta expresada por la siguiente relación [12] [13]
depende de las segundas derivadas de las
coordenadas, por lo tanto la ecuación de Euler-Lagrange para sistemas
continuos esta expresada por la siguiente relación [12] [13]
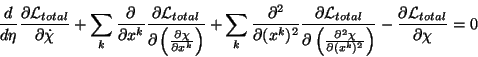 |
(4.39) |
De este modo, al realizar las variaciones correspondientes a cada variable
se obtiene el siguiente conjunto de ecuaciones diferenciales parciales.
- Variación de
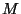 :
:
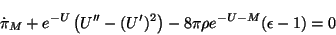 |
(4.40) |
- Variación de
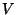 :
:
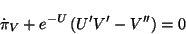 |
(4.41) |
- Variación de
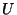 :
:
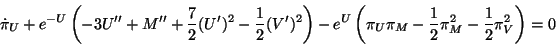 |
(4.42) |
- Variación de
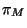 :
:
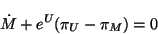 |
(4.43) |
- Variación de
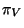 :
:
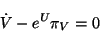 |
(4.44) |
- Variación de
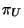 :
:
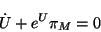 |
(4.45) |
Conbinando las ecs. 4.40 y 4.45 se llega a la
expresión
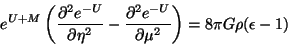 |
(4.46) |
Esta ecuación también puede obtenerse al sumarse las ecs. 4.33 y 4.36 las cuales se obtienen directamente de las
ecuaciones de Einstein.
Sustituyendo las ecs. 4.43, 4.44 y 4.45 en la ecuación de constricción 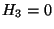 dada por
dada por
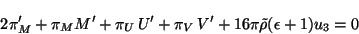 |
(4.47) |
se obtiene que
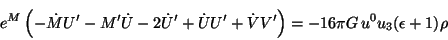 |
(4.48) |
este resultado no es otra cosa más que la ecuación de Einstein 4.37.
Combinando las ecuaciones 4.41 y 4.44 se llega a
la expresión
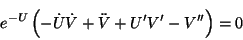 |
(4.49) |
tal ecuación se puede obtener al restar de la ec. 4.35 la ec.
4.34, las cuales fueron obtenidas directamente de la ecuación de
campo de Einstein.




Next: Buscando la solución general
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Ecuaciones de Einstein
Índice General
enrique pazos
2000-09-27