



Next: Lagrangiano de la geometría
Up: tglo
Previous: Lagrangiano de los campos
Índice General
En este capítulo se aplicarán los conceptos desarrollados
anteriormente a una métrica dada, que tiene la forma
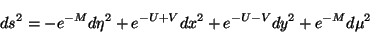 |
(4.1) |
en donde 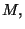
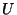 y
y 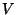 son funciones de
son funciones de 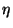 y
y 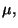 las cuales a su
vez representan a las coordenadas tipo tiempo y tipo
espacial respectivamente [11].
Lo que se quiere encontrar es un lagrangiano a partir del cual, se puedan
obtener las ecuaciones que rigen el comportamiento de los campos en
presencia de materia. Como se observa en la sección 3.1, este
lagrangiano está compuesto por dos partes, aquella que corresponde a la
geometría y la que corresponde a la materia. A continuación se
presentan los cálculos necesarios para encontrar el lagrangiano total,
dado por la ec. 3.4.
las cuales a su
vez representan a las coordenadas tipo tiempo y tipo
espacial respectivamente [11].
Lo que se quiere encontrar es un lagrangiano a partir del cual, se puedan
obtener las ecuaciones que rigen el comportamiento de los campos en
presencia de materia. Como se observa en la sección 3.1, este
lagrangiano está compuesto por dos partes, aquella que corresponde a la
geometría y la que corresponde a la materia. A continuación se
presentan los cálculos necesarios para encontrar el lagrangiano total,
dado por la ec. 3.4.
Subsecciones
enrique pazos
2000-09-27