



Next: Lagrangiano de la materia
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: APLICACIÓN DEL FORMALISMO ADM
Índice General
La densidad lagrangiana para la parte de la geometría está dada por
la ec. 3.25
![\begin{displaymath}
\mathrm{\mathcal{L}}_{geo}=\pi ^{ij}\dot{g}_{ij}+N\sqrt{^{\...
...2-\pi ^{ij}\pi _{ij}\right) \right] +2N_i\pi
_{\mid j}^{ij}
\end{displaymath}](img381.gif) |
(4.2) |
de la ec. 4.1 se observa que la trimétrica está dada como
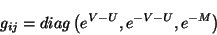 |
(4.3) |
y su derivada respecto del tiempo será
El primer término de la ec. 4.2,
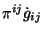 es
es
esta última expresión sugiere la introducción de las siguientes
variables
sustituyendo estos nuevos momentos en la ec. 4.4 se obtiene que
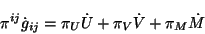 |
(4.6) |
De las ecs. 4.5 se puede encontrar que los momentos originales 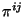 en función de los nuevos momentos están dados por
en función de los nuevos momentos están dados por
De la ec. 3.14, se obtiene que
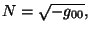 es decir
es decir
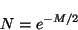 |
(4.8) |
El determinante de la trimétrica es igual a producto de cada uno de los
elementos de la matriz diagonal 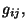 esto es
esto es
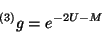 |
(4.9) |
El escalar de curvatura
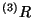 se calcula a partir de la ec.
2.31, sumando únicamente sobre las componentes espaciales del
tensor de Ricci mixto
se calcula a partir de la ec.
2.31, sumando únicamente sobre las componentes espaciales del
tensor de Ricci mixto 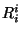 . Al hacer esto se encuentra que
. Al hacer esto se encuentra que
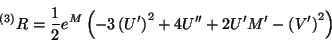 |
(4.10) |
el cálculo detallado de
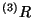 se puede ver en el
Apéndice.
Desarrollando el término
se puede ver en el
Apéndice.
Desarrollando el término 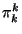 se tiene lo siguiente
se tiene lo siguiente
sustituyendo 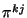 por los momentos de las ecs. 4.7,
así como los valores de
por los momentos de las ecs. 4.7,
así como los valores de 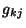 , la expresión anterior se convierte
en
, la expresión anterior se convierte
en
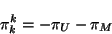 |
(4.12) |
De la misma manera, el término
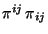 toma la forma
toma la forma
en donde también se han utilizado las ecs. 4.7.
Por último, el término
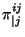 se calcula de la
siguiente manera
se calcula de la
siguiente manera
debido a que 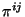 depende sólo de
depende sólo de 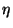 y
y 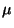 las derivadas
con respecto a
las derivadas
con respecto a 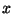 e
e 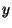 son idénticas a cero, quedando solamente la que
corresponde a
son idénticas a cero, quedando solamente la que
corresponde a 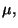 es decir,
es decir, 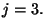 Además, los símbolos de
Christoffel diferentes de cero son
Además, los símbolos de
Christoffel diferentes de cero son
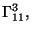
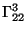 y
y
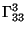 (ver Apéndice). De lo anterior se deduce que la
única componente diferente de cero de
(ver Apéndice). De lo anterior se deduce que la
única componente diferente de cero de
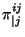 es la que se
obtiene cuando
es la que se
obtiene cuando 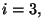 por lo tanto
por lo tanto
en donde se ha utilizado las ecs. 4.7.
Utilizando los resultados de las ecs. 4.6, 4.8, 4.9, 4.10, 4.12, 4.13 y 4.15, al sustituirlos en la
ec. 4.2 se tiene que
Esta expresión es la densidad lagrangiana en el espacio vacío, es
decir, la parte que involucra a la geometría del espacio.




Next: Lagrangiano de la materia
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: APLICACIÓN DEL FORMALISMO ADM
Índice General
enrique pazos
2000-09-27