



Next: RECOMENDACIONES
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Solución para un caso
Índice General
- Los sistemas que presentan constricciones (mediante multiplicadores
de Lagrange), poseen la característica de que éstas se pueden elegir
apropiadamente para obtener sus propiedades físicas.
- La introducción de las variables ADM en la métrica puede
ser aprovechada para hacer análisis numéricos de problemas
complejos. Esto se debe a que las variables
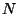 y
y 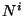 son funciones de
norma, es decir, que son funciones que se escogen según la manera en la
que se quiera foliar el espacio-tiempo.
son funciones de
norma, es decir, que son funciones que se escogen según la manera en la
que se quiera foliar el espacio-tiempo.
- Las ecuaciones que se obtienen del formalismo ADM son
combinaciones de aquellas que se obtienen mediante la ecuación de campo
de Einstein. A la vez, las primeras son más sencillas que estas
últimas, ya que presentan algunas simetrías del problema.
- Con la formulación lagrangiana de la gravitación, se puede
saber cuáles son las ecuaciones que representan constricciones en las
variables. Esto se debe a la forma misma del lagrangiano. Tal hecho no
ocurre con las ecuaciones de Einstein, ya que no hay distinción en la
procedencia de cada una de ellas.
- El sistema de ecuaciones resultante para el modelo propuesto es
altamente complejo y no admite una solución general. Únicamente
haciendo simplificaciones posteriores se puede encontrar una solución
exacta. Lo recalcable de este modelo es que presenta un comportamiento de
ondas entrantes y salientes en las componentes de la métrica. Algunos
ejemplos fueron graficados para mostrar esto último.
- Como se menciona en la introducción de este trabajo, se pueden
tener sistemas físicos gobernados por una función de densidad
lagrangiana
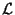 . De ella, (mediante transformaciones de Lagrange)
se obtiene una densidad hamiltoniana
. De ella, (mediante transformaciones de Lagrange)
se obtiene una densidad hamiltoniana 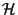 ; la cual, desde el punto
de vista ADM, viene siendo una constricción:
; la cual, desde el punto
de vista ADM, viene siendo una constricción: 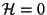 . Este
hamiltoniano debe ser escrito en función de los momentos canónicos.
En este punto, se puede realizar la cuantización del sistema de la
manera usual, es decir, eligiendo una representación de estos momentos.
Usualmente es de la forma
. Este
hamiltoniano debe ser escrito en función de los momentos canónicos.
En este punto, se puede realizar la cuantización del sistema de la
manera usual, es decir, eligiendo una representación de estos momentos.
Usualmente es de la forma
además se debe elevar la constricción 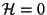 a un operador
aplicado a una función de onda, es decir,
a un operador
aplicado a una función de onda, es decir,
de este modo se tiene una ecuación cuántica del sistema estudiado.
Para algunos modelos cosmológicos, esta ecuación ha sido resuelta
desde este punto de vista.




Next: RECOMENDACIONES
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Solución para un caso
Índice General
enrique pazos
2000-09-27