Next: CONCLUSIONES
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Buscando la solución general
Índice General
Al elegir un sistema de coordenadas co-movil, se tiene que 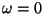 , con
lo cual, las componentes de la cuadri-velocidad son
, con
lo cual, las componentes de la cuadri-velocidad son 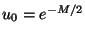 y
y 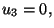 es decir que la velocidad del fluido de materia será
es decir que la velocidad del fluido de materia será
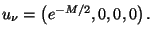 Con esta simplificación, las ecs. 4.52 y 4.53 se reducen
a
Con esta simplificación, las ecs. 4.52 y 4.53 se reducen
a
Al resolver estas ecuaciones y despejar la densidad 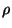 se encuentra que
las soluciones son
se encuentra que
las soluciones son
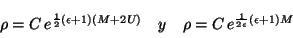 |
(4.59) |
respectivamente, donde 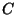 es una constante arbitraria. Debido que las dos
soluciones para
es una constante arbitraria. Debido que las dos
soluciones para 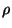 deben ser equivalentes, al igualarlas se tiene que
deben ser equivalentes, al igualarlas se tiene que
Esta ecuación expresa que el campo 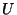 depende en forma lineal del campo
depende en forma lineal del campo
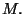 Tomando los resultados de las ecs. 4.59 y 4.60 para luego
sustituirlos en la ec. 4.46 se llega a que
Tomando los resultados de las ecs. 4.59 y 4.60 para luego
sustituirlos en la ec. 4.46 se llega a que
esta es una ecuación de onda no homogénea la cual acepta una
solución exacta de la forma
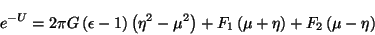 |
(4.62) |
donde 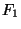 y
y 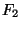 son funciones arbitrarias en sus argumentos. De la
ecuación anterior se obtiene la solución para la función
son funciones arbitrarias en sus argumentos. De la
ecuación anterior se obtiene la solución para la función 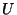 se
expresa como
se
expresa como
![\begin{displaymath}
U=-\ln \left[ 2\pi G\left( \epsilon -1\right) \left( \eta ^...
...\eta \right) +\allowbreak F_2\left( \mu -\eta \right) \right]
\end{displaymath}](img571.gif) |
(4.63) |
con lo cual, de las ec. 4.60 y la anterior se encuentra que la
solución para la función 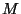 tiene la siguiente forma
tiene la siguiente forma
![\begin{displaymath}
M=\frac{2\epsilon }{\epsilon -1}\ln \left[ 2\pi G\left( \ep...
...eta \right) +\allowbreak
F_2\left( \mu -\eta \right) \right]
\end{displaymath}](img572.gif) |
(4.64) |
La solución para para la función 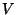 depende de la forma que tengan
las funciones arbitrarias
depende de la forma que tengan
las funciones arbitrarias 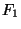 ,
, 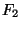 ,
, 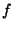 y
y 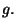 Las condiciones de
frontera se podrían escoger de tal manera que
Las condiciones de
frontera se podrían escoger de tal manera que 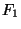 y
y 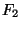 sean
funciones sencillas y con esto poder integrar las ecs. 4.51.
Si se asume que la primera de las ecs. 4.51 no tiene una dependencia
explícita de
sean
funciones sencillas y con esto poder integrar las ecs. 4.51.
Si se asume que la primera de las ecs. 4.51 no tiene una dependencia
explícita de 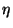 y la segunda no depende explícitamente de
y la segunda no depende explícitamente de 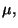 la ec. 4.49 queda satisfecha. Esto significa que ambas derivadas
parciales son cero. En base a esto se puede proponer que
la ec. 4.49 queda satisfecha. Esto significa que ambas derivadas
parciales son cero. En base a esto se puede proponer que
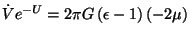 , expresión en la cual
no aparece la variable
, expresión en la cual
no aparece la variable 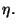 Esto se puede reescribir de la siguiente
manera
Esto se puede reescribir de la siguiente
manera
La expresión que aparece entre corchetes es claramente 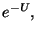 cuando
se elige a las funciones arbitrarias
cuando
se elige a las funciones arbitrarias 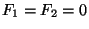 . Por lo tanto, el factor
restante es
. Por lo tanto, el factor
restante es 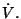 Al integrar respecto de
Al integrar respecto de 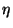 se encuentra que
se encuentra que
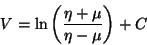 |
(4.66) |
donde 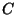 es una constante de integración. El mismo resultado se obtiene
al considerar que
es una constante de integración. El mismo resultado se obtiene
al considerar que
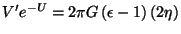 .
Se tiene entonces que la solución para este caso especial es
.
Se tiene entonces que la solución para este caso especial es
En las siguientes gráficas se muestra el comportamiento de las
componentes de la métrica. La figura 1 resulta de elegir las funciones
arbitrarias como
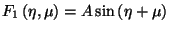 y
y
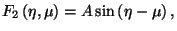 tomando una amplitud
tomando una amplitud 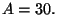 Así mismo, el valor de la constante
Así mismo, el valor de la constante 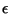 ha sido tomado como
ha sido tomado como 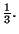 En modelos cosmológicos
isotrópicos, esto representa un universo dominado por radiación. Las
figuras 2, 3, 4 y 5 corresponden al caso particular en que
En modelos cosmológicos
isotrópicos, esto representa un universo dominado por radiación. Las
figuras 2, 3, 4 y 5 corresponden al caso particular en que 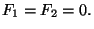
Figura 4.1:
Componente 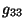 con
con 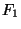 y
y 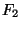 diferentes de cero.
diferentes de cero.
![\includegraphics[height=4in, width=5.5in]{g332.ps}](img595.gif) |
Figura 4.2:
Componente 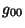 .
.
![\includegraphics[height=4in, width=5.5in]{g00.ps}](img596.gif) |
Figura 4.3:
Componente  .
.
![\includegraphics[height=4in, width=5.5in]{g11.ps}](img597.gif) |
Figura 4.4:
Componente 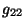 .
.
![\includegraphics[height=4in, width=5.5in]{g22.ps}](img598.gif) |
Figura 4.5:
Componente 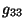 .
.
![\includegraphics[height=4in, width=5.5in]{g33.ps}](img599.gif) |




Next: CONCLUSIONES
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Buscando la solución general
Índice General
enrique pazos
2000-09-27
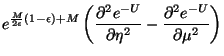
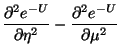
![$\displaystyle \left( \frac 1{\eta +\mu }-\frac 1{\eta -\mu }\right) \left[ 2\pi G\left(
\epsilon -1\right) \left( \eta ^2-\mu ^2\right) \right]$](img578.gif)