



Next:Derivada
covarianteUp:DE
LA RELATIVIDAD ESPECIALPrevious:TensoresÍndice
General
Símbolos de Christoffel
Un vector se desplaza paralelamente cuando no se cambia su magnitud ni
dirección. Cuando se desplaza paralelamente un vector en coordenadas
cartesianas, las componentes de los vectores permanecen sin cambio alguno.
En algunos sistemas de coordenadas esto no es así y al mover un
vector paralelamente, de un punto a otro, sus componentes cambian. El símbolo
de Christoffel 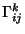 se define para facilitar la descripción de los desplazamientos paralelos.
Si un vector
se define para facilitar la descripción de los desplazamientos paralelos.
Si un vector 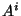 es paralelamente desplazado sobre un intervalo
es paralelamente desplazado sobre un intervalo 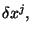 el cambio en sus componentes
el cambio en sus componentes 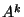 está determinado por el símbolo de Christoffel:
está determinado por el símbolo de Christoffel:
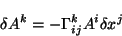 |
(2.16) |
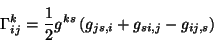 |
(2.17) |
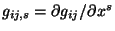 .
La ec. 2.16
expresa el cambio en las componentes de un vector contravariante al ser
desplazado paralelamente. Una expresión similar se puede encontrar
para el caso en que el vector sea covariante. Considerando el hecho que
el producto interior de dos vectores es un invariante, se puede decir que
.
La ec. 2.16
expresa el cambio en las componentes de un vector contravariante al ser
desplazado paralelamente. Una expresión similar se puede encontrar
para el caso en que el vector sea covariante. Considerando el hecho que
el producto interior de dos vectores es un invariante, se puede decir que
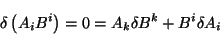 |
(2.18) |
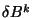 de la ec. 2.16
y despejando
de la ec. 2.16
y despejando 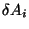 se obtiene que
se obtiene que
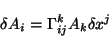 |
(2.19) |
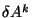 y
y 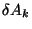 no son vectores debido a que
no son vectores debido a que 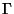 no es un tensor. En coordenadas cartesianas
no es un tensor. En coordenadas cartesianas 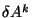 es igual a cero pero no lo es en coordenadas polares. Un vector que es
cero en un sistema de coordenadas no puede ser diferente de cero en otro
sistema. El mismo argumento se aplica a los símbolos de Christoffel.
En un sistema cartesiano éstos son iguales a cero, pero no lo son
en coodenadas polares. [3]
es igual a cero pero no lo es en coordenadas polares. Un vector que es
cero en un sistema de coordenadas no puede ser diferente de cero en otro
sistema. El mismo argumento se aplica a los símbolos de Christoffel.
En un sistema cartesiano éstos son iguales a cero, pero no lo son
en coodenadas polares. [3]




Next:Derivada
covarianteUp:DE
LA RELATIVIDAD ESPECIALPrevious:TensoresÍndice
General
enrique pazos 2000-09-27